Лекция 18. Поляризация электромагнитных волн. Закон Малюса. Закон Брюстера.
Поляризованнымназывается электромагнитное излучение, в котором колебания вектора Е упорядочены. Например, в плоско- поляризованной волне световой вектор колеблется, все время оставаясь параллельным некоторой прямой в пространстве. Поэтому в процессе распространения все его мгновенные положения лежат в одной плоскости, называемой плоскостью колебаний. Естественный свет не является поляризованным, в нем колебания различных направлений беспорядочно сменяют друг друга.
Покажем, что естественный свет можно представить в виде суммы двух некогерентных электромагнитных волн, поляризованных во взаимно перпендикулярных плоскостях. Для этого сначала рассмотрим результат сложения таких волн. Пусть вдоль оси z, направленной "на нас" распространяются два колебания, происходящие вдоль осей х и у и сдвинутые по фазе на d
Ex =A1cos wt и Ey =A2cos (wt+d).
|
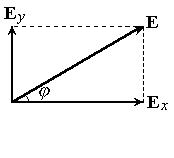
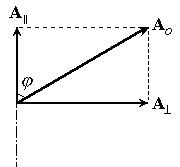
Результирующая напряженность является векторной суммой: Е=Еx+Еy (рис.65). Угол j между векторами Е и Еx определяется из очевидного соотношения:
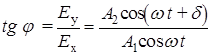 . (199)
. (199)
| Рис.65 |
Варьируя d можно произвольно менять j, что позволяет описать любые направления вектора Е. Рассмотрим частные случаи. Если d=0 (или p), то 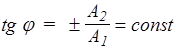 , следовательно, результирующее колебание вектора Е происходит в фиксированном направлении - волна плоскополяризована. Если d=±p/2, то
, следовательно, результирующее колебание вектора Е происходит в фиксированном направлении - волна плоскополяризована. Если d=±p/2, то 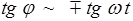 . Тогда плоскость колебаний поворачивается вокруг направления распространения волны с угловой скоростью w. (В оптике это направление называют просто лучом.) Причем в проекции на плоскость ху конец вектора Е описывает эллипс (так как колебания Еx и Еy взаимно перпендикулярны). Такой свет называется эллиптически поляризованным. В частности, когда А1=А2, эллипс превращается в окружность, и тогда свет называется поля-ризованным по кругу.
. Тогда плоскость колебаний поворачивается вокруг направления распространения волны с угловой скоростью w. (В оптике это направление называют просто лучом.) Причем в проекции на плоскость ху конец вектора Е описывает эллипс (так как колебания Еx и Еy взаимно перпендикулярны). Такой свет называется эллиптически поляризованным. В частности, когда А1=А2, эллипс превращается в окружность, и тогда свет называется поля-ризованным по кругу.
Поляризаторы. Идеальным поляризатором называется устройство, которое пропускает колебания, параллельные так называемой плоскости поляризатора, и задерживает колебания, перпендикулярные этой плоскости. Если поляризатор не идеален, то получают частично поляризованный свет. Если частично поляризованный свет пропустить через поляризатор и вращать последний вокруг направления луча, то в зависимости от угла между плоскостями колебаний и поляризатора интенсивность прошедшего света будет меняться от Jmax до Jmin; Jmax соответствует параллельности плоскости преобладающих колебаний и плоскости поляризатора; Jmin - перпендикулярности. Угол поворота поляризатора между этими положениями равен p/2. Частично поляризованный свет характеризуют степенью поляризации Р
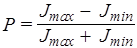 . (200)
. (200)
|
Для плоскополяризованного света Р=1 (так как Jmin=0); для естественного - Р=0 (так как Jmax=Jmin). К эллиптически поляризованному свету понятие степени поляризации не применимо.
| Рис.66 |
Закон Малюса. Пусть на поляризатор падает плоскополяризованный свет амплитуды А0 и интенсивности J0. Выбор пары направлений (ох, оу), по которым можно разложить световой вектор, произволен. Однако при прохождении света через поляризатор целесообразно выбрать одно из них параллельно оси поляризатора, тогда другое будет ей перпендикулярно (рис.66): А||=A0 cosj, А^= A0 sinj, где А0 - амплитуда падающей на поляризатор волны. Первое колебание пройдет через прибор, второе будет задержано. Интенсивность J прошедшей через поляризатор волны (рис.67) будет пропорциональна 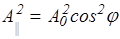 , т.е.
, т.е.
|
J = Jocos2j, (201)
которое называется законом Малюса. Интенсивность плоскополяризованного света убывает пропорционально квадрату косинуса угла между плоскостями колебаний и поляризатора.
| Рис.67 |
|
Практический интерес представляет последовательное прохождение естественного света через два поляризатора, так как эта ситуация реализована во многих оптических приборах. Пусть угол между поляризаторами j. Из первого поляризатора выйдет свет, интенсивность которого J0 составит половину интенсивности естественного; из второго, согласно (201), выйдет свет с интенсивностью J0 cos2j. Поэтому интенсивность света J после прохождения обоих поляризаторов
J=1/2(Jестcos2j).
Интенсивность максимальна при j=0, когда поляризаторы параллельны, и равна 1/2(Jест). При j=p/2 интенсивность равна нулю - скрещенные поляризаторы вообще не пропускают свет.
| Рис.68 |
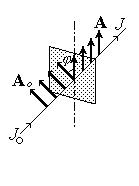
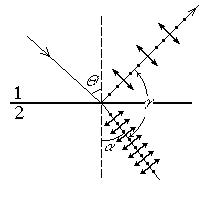
Закон Брюстера. При падении света на границу раздела двух диэлектриков отраженный и преломленный лучи оказываются частично поляризованными: в отраженном преобладают колебания, перпендикулярные плоскости падения, в преломленном - параллельные (рис.68). В данном случае плоскость падения совпадает с плоскостью рисунка. Степень поляризации зависит от угла падения. Угол падения QБр, удовлетворяющий условию
tgQБр = n12, (202)
где n12 - показатель преломления второй среды относительно первой называется углом Брюстера. Угол Брюстера - это такой угол падения, при котором отраженный луч полностью поляризован, а степень поляризации преломленного луча максимальна. Соотношение (202) называется законом Брюстера. При падении под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны, таккак sinQБр/cosQБр=n12 и sinQБр/sinQБр=n12, => sinQБр=cosQБр=sin(p/2-QБр), => a=p/2-QБр, => a+QБр=p/2, => g=p/2.
Дата добавления: 2015-08-14; просмотров: 2683;
