Лекция 14. Энергия магнитного поля. Уравнения Максвелла в веществе

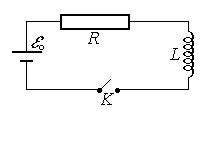
Рассмотрим цепь, содержащую активное сопротивление R, катушку индуктивности L и источник эдс e_o (рис.49). При замыкании ключа К ток начнет возрастать, вследствие этого появится эдс самоиндукции e_s. По закону Ома, RI=e_o+e_s, следовательно,

e_o= RI - e_s .

Умножая обе части на Idt, получим

e_o Idt = RI² dt - e_s Idt,

где левая часть представляет собой работу сторонних сил dА*, первое слагаемое справа - джоулево тепло. Последнее слагаемое равно IdФ (так как e_S=-dФ/dt). Таким образом,

dА* =dQ+IdФ,

следовательно, dА*>dQ, а часть работы (IdФ=ILdI) совершается против эдс самоиндукции. За счет этой работы контур накапливает энергию, которую вычислим, интегрируя последнее выражение

W = 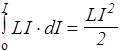. (150)

Выразим энергию магнитного поля через В. Действительно, L=mm_on²V, как индуктивность длинного соленоида, поэтому

W = .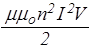

Но так как для соленоида В=mm_onI, и B=mm_oH, следовательно,

,

где слева стоит энергия поля в единице объема, т.е. плотность энергии. Расчет показывает, что это верно и в векторном виде

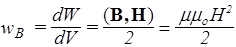, (151)

где w_B - плотность энергии магнитного поля, которая для неоднородного поля равна производной: w_B=dW/dV.

Уравнения Максвелла для среды в интегральной форме. Выпишем уравнения Максвелла для среды в интегральной форме в виде таб.2, где в правой колонке дадим их формулировки.

Уравнения Максвелла для среды в интегральной форме. Таблица 2

I		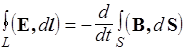Циркуляция вектора Е по любому замкнутому контуру равна минус производной по времени от магнитного потока через любую поверхность, ограниченную этим контуром. Под Е понимается как вихревое, так и электростатическое поле
II		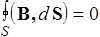Поток вектора В сквозь любую замкнутую поверхность равен нулю
III		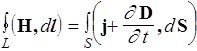Циркуляция вектора Н по любому замкнутому контуру равна полному току (проводимости и смещения) через любую поверхность, ограниченную данным контуром
IV		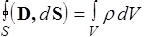Поток вектора D сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью

По форме уравнения Максвелла для вещества и вакуума идентичны. Однако для описания электрического и магнитного полей в вакууме введение векторов D и Н не являлось принципиально необходимым. Рассуждения, с помощью которых мы пришли к уравнениям Максвелла, не могут претендовать на роль доказательств. Эти уравнения в общем случае нельзя "вывести" - они являются основными аксиомами электродинамики.

Уравнения Максвелла в веществе в дифференциальной форме. В принципе эти уравнения уже были нами сформулированы. Выпишем их еще раз, используя параллельно оператор набла

I. , .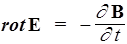

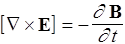II. div B= 0, .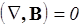

III. , ,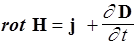

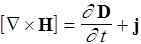IV. div D =r, (Ñ,D) = r.

В этой форме уравнения утверждают следующее. Электрическое поле может возникнуть по двум причинам. Во-первых, его источниками являются электрические заряды (и сторонние, и связанные - это следует из последнего уравнения, где D=e_оЕ+Р и (Ñ,P)=-r', следовательно, (Ñ,E)~ r+r'); во-вторых,- переменное магнитное поле. Как видно из уравнения III, магнитное поле может порождаться движущимися зарядами и переменными электрическими полями: так как Н=m₀B-J и [Ñ´J]=j', следовательно, [Ñ´B]~j+j'+¶Р/¶t+e_о¶E/¶t. Первые три тока связаны с движением зарядов, последний - с изменяющимся во времени электрическим полем Е. Источников магнитных зарядов не существует (это показывает уравнение II).

Материальные уравнения. Фундаментальные уравнения Максвелла не составляют полной системы уравнений: их недостаточно для нахождения полей по заданным распределениям зарядов и токов. Для этого их необходимо дополнить соотношениями, характеризующими свойства среды. Эти соотношения называются материальными уравнениями.

Материальные уравнения просты (и нам уже знакомы) в случае достаточно слабых электромагнитных полей, медленно меняющихся в пространстве и во времени. Для изотропных сред, несодержащих сегнетоэлектриков и ферромагнетиков, материальные уравнения имеют вид

D= ee_oE, B= mm_oH, j= s(E+ E*).

Величины e, m и s характеризуют электрические и магнитные свойства среды; E* - напряженность поля сторонних сил.