Лекция 12. Условия на границе раздела диэлектриков. Энергия электрического поля
Введение вспомогательного вектора D позволило вынести описание поляризации диэлектрика за рамки уравнений Максвелла. Поле вектора D можно изображать с помощью силовых линий, направление и густота которых определяются также, как и для вектора Е. Однако линии вектора Е могут начинаться как на свободных, так и на связанных зарядах. Поскольку источниками вектора D являются только свободные заряды, на них начинаются и заканчиваются линии вектора D. Через области поля, содержащие связанные заряды, линии вектора D проходят, не прерываясь.
В качестве иллюстрации полезности вектора D рассмотрим пример. Пусть точечный свободный заряд q находится в центре шара радиуса R из однородного изотропного диэлектрика с диэлектрической проницаемостью e. Найдем напряженность Е поля как функцию расстояния r от центра.
В этой задаче невозможно воспользоваться теоремой Гаусса для вектора Е, несмотря на то, что симметрия задачи располагает к этому, потому что не дано распределение связанного заряда. Однако поток вектора D зависит только от свободного заряда, который дан. Поэтому сначала применим теорему Гаусса для вектора D, выбрав в качестве гауссовой поверхности сферу произвольного радиуса r
|
4pr2D = q.
Подставляя D=eeoE для r£R и D=eoE для r>R, получаем
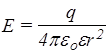 при r£R;
при r£R;
| Рис.39 |
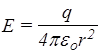 при r>R.
при r>R.
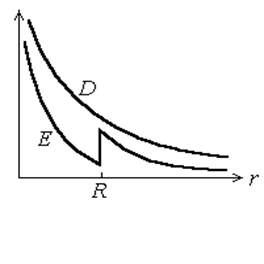
Из сопоставления последних двух формул (они отличаются множителем e в знаменателе) видно, что при r=R величина Е испытываетскачок. Графики зависимостей Е и D от r представлены на рис.39.
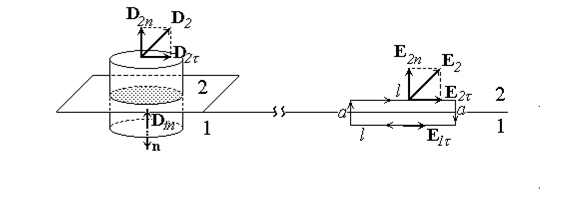
Условия для векторов E и D на границе раздела диэлектриков. Выясним, как связаны компоненты векторов E и D по разные стороны от границы диэлектриков 1 и 2 (рис.40). Пусть S - цилиндрическая поверхность пренебрежимо малой высоты. Поток вектора D через S равен нулю, так как внутри нее нет свободных зарядов. Поток через боковую поверхность очень мал, так как мала ее площадь. Поэтому поток через нижнее основание равен потоку через верхнее основание: 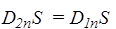 , Þ
, Þ
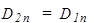 . (129)
. (129)
|
| Рис.40 Рис.41 |
Таким образом, нормальная составляющая Dnсохраняется.
Рассмотрим теперь прямоугольный замкнутый контур (рис.41), сторона которого l параллельна границе раздела, а высота а много меньше длины. Так как циркуляция вектора Е электростатического поля 
 равна нулю, для изображенного на рисунке контура это значит, что
равна нулю, для изображенного на рисунке контура это значит, что 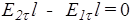 , следовательно,
, следовательно,
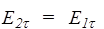 , (130)
, (130)
т.е. при переходе через границу раздела диэлектриков сохраняется тангенциальная составляющая Et.
Покажем, что величины составляющих En и Dt меняются на границе раздела. Поскольку векторы Е и D связаны соотношением (128), и Dn сохраняется, следовательно, e2E2n = e1E1n, или
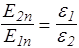 . (131)
. (131)
Аналогично из (128) и сохранения Еt следует, что
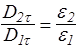 . (132)
. (132)
Из граничных условий в частности следует, что если диэлектрик заполняет все пространство, занимаемое полем (например, в плоском конденсаторе), то напряженность поля Е в нем будет в e раз меньше, чем в отсутствие диэлектрика.
|
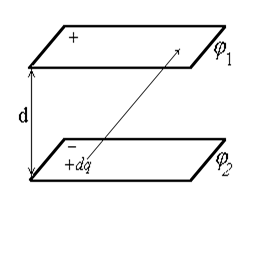
| Рис.42 |
Энергия электрического поля. Рассмотрим процесс зарядки конденсатора (рис.42). Пусть верхняя пластина заряжена положительно зарядом +q до потенциала j1, а нижняя-- зарядом -q до j2. Работа против сил поля при переносе заряда dq>0 с нижней пластины на верхнюю идет на увеличение энергии взаимодействия зарядов
dW = - dA = dq(j1 -j2) = dq U.
Выразим напряжение U через емкость С: U=q/С, тогда dW=qdq/C. Интегрируя, получаем энергию электрического поля заряженного конденсатора
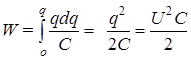 . (133)
. (133)
Как известно, емкость плоского конденсатора С=eeoS/d, где S - площадь одной пластины, d - расстояние между пластинами. Подставим С в (133) и учтем, что напряженность однородного поля между пластинами равна Е=U/d
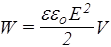 ,
,
где V=Sd - объем пространства между пластинами. Отношение W/V характеризует энергию единицы объема и называется плотностью энергии электрического поля
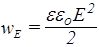 (134)
(134)
Если поле неоднородно, то плотность энергии электрического поля равна производной wE=dW/dV. Учитывая, что Е=D/eeо, a D=eоЕ+Р запишем
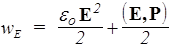 . (135)
. (135)
Полученное выражение представляет собой сумму плотности электрической энергии в вакууме и плотности энергии поляризации диэлектрика. Следовательно, электрическая энергия локализована в самом поле: как там, где есть вещество, так и там, где его нет. Однако если поле стационарно, то при исчезновении порождающих его зарядов, исчезает и само поле. Независимо от породивших их зарядов могут существовать только переменные поля.
Дата добавления: 2015-08-14; просмотров: 1557;
