Магнитное поле в веществе.

Магнетики. Намагничивание магнетиков. Вектор намагниченности.

В веществе магнитное поле возбуждается не только электрическими токами, текущими по проводам, но и движением заряженных частиц внутри самих атомов и молекул. Поэтому результирующее поле в веществе является суперпозицией поля, созданного токами 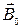, и поля, обусловленного зарядами самого вещества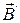

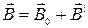. ( 2.10.1 )

В дальнейшем любое физическое тело, рассматриваемое с точки зрения его магнитных свойств, будет называться магнетиком. (Магнетики могут быть и диэлектриками и проводниками). Поскольку стационарные магнитные поля могут порождаться только движущимися электрическими зарядами, то происхождение дополнительного магнитного поля сязывают с незатухающими и неразрушаемыми кольцевыми токами (микротоками), циркулирующими внутри микрочастиц вещества (например, электроны вращаются вокруг атомных ядер по замкнутым орбитам). Впервые это положение как гипотеза было выдвинуто в 1820 г. А.Ампером. Эти микротоки (микроконтуры с токами) обладают магнитным моментом. В отсутствие внешнего магнитного поля микротоки ориентированы беспорядочно, вследствие чего создаваемое ими результирующее поле равно нулю. Под действием внешнего поля их магнитные моменты приобретают преимущественную ориентацию в одном направлении. Этот процесс называют намагничиванием магнетика. Для характеристики этого процесса вводят величину, называемую вектором намагниченности (или намагниченностью) – это суммарный магнитный момент единицы объема

, (2.10.2 )

где 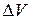- физически бесконечно малый объем, а в числителе стоит сумма магнитных моментов в этом объеме. Из вышесказанного следует, что в отсутствие внешнего поля намагниченность магнетика равна нулю.

Намагничивание среды приводит к появлению так называемых токов намагничивания. (Обычные токи, текущие по проводам, называют токами проводимости). Для пояснения рассмотрим магнетик в форме прямого цилиндра, находящегося в магнитном поле, вектор индукции которого параллелен образующей цилиндра. На рис 2.10.1 показано сечение этого магнетика, перпендикулярное вектору индукции. Молекулярные токи в намагниченном магнетике текут согласовано (по часовой стрелке, как показано на рисунке) и молекулярные токи соседних молекул в местах их соприкосновения текут в противоположных направлениях и макроскопически взаимно компенсируют друг друга. Некомпенсированными остаются только молекулярные токи, выходящие на наружную боковую поверхность цилиндра. Эти токи складываются в макроскопический поверхностный ток , циркулирующий по боковой поверхности цилиндра. Этот ток возбуждает такое же макроскопическое поле 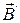, которое, как видно из рисунка усиливает внешнее поле.

Теорема о циркуляции магнитного поля в веществе. Напряженность магнитного поля. Магнитная проницаемость.

При расчете циркуляции вектора по любому замкнутому контуру в магнетике нужно учитывать и токи проводимости 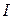, создающие поле, и токи намагничивания

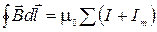. (2.10.3 )

Можно показать, что циркуляция вектора намагниченности равна алгебраической сумме токов намагничивания, охватываемых этим контуром

.

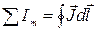Тогда .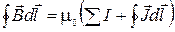

Перенеся второе слагаемое из правой части в левую и приняв во внимание, что интегралы берутся по одному и тому же контуру, получим

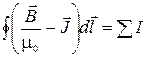. (2.10.4 )

Величину, стоящую в скобках под интегралом, называют напряженностью магнитного поля 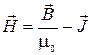. ( 2.10.5 )

Таким образом, теорема о циркуляции магнитного поля в магнетиках гласит: циркуляция вектора 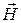по произвольному замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых контуром

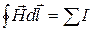. (2.10.6 )

Заметим, что вектор напряженности вводят для упрощения расчета магнитных полей, поскольку циркуляция 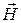определяется только токами проводимости.

Мы уже знаем, что вектор намагниченности связан с создающим ее полем. Однако, 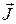принято связывать с 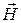. Для изотропных магнетиков

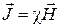. (2.10.7 )

Скалярная безразмерная величина 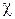называется магнитной восприимчивостью. Тогда из (2.10.5) и (2.10.7) следует

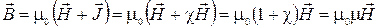, (2.10.8 )

где 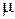- магнитная проницаемость среды. В отличие от диэлектрической восприимчивости, которая всегда положительна, магнитная восприимчивость может быть и положительной и отрицательной. В соответствии с этим магнетики делят на парамагнетики ( 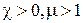) и диамагнетики ( ).

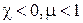Принимая во внимание (2.10.8) для поля в бесконечном соленоиде, запишем , .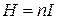

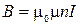Граничные условия на границе магнетиков.

При переходе через границу двух сред характеристики магнитного поля (так же как и электрического) изменяются. Для получения соотношения, связывающего векторы по обе стороны границы раздела используем теорему Гаусса для магнитного поля (2.9.3). Решая задачу так же как для вектора 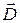(лекция 5), получим

. ( 2.10.9 )

Аналогично, из теоремы о циркуляции вектора 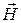(2.10.6) при условии отсутствия токов проводимости, текущих по границе раздела сред, проводя рассмотрение как для вектора 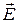(лекция 5), получим

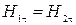. ( 2.10. 10 )

Диа-, пара-, ферромагнетики.

По своим магнитным свойствам вещества можно разделить на слабомагнитные и сильно магнитные. К слабо магнитным относятся диамагнетики и парамагнетики, к сильномагнитным – ферромагнетики, антиферромагнетики и ферримагнетики. В пара- и диамагнетиках, не находящихся в магнитном поле, отсутствует намагниченность в любом малом объеме вещества. Они характеризуются однозначной зависимостью между вектором намагничивания и напряженностью магнитного поля (в слабых полях эта зависимость линейна.

Парамагнетизм наблюдается у тех веществ, атомы которых обладают собственными магнитными моментами. Пока нет магнитного поля, атомы совершают беспорядочное тепловое движение и их магнитные моменты ориентированы беспорядочно. В этом случае тело не намагничено. В магнитном поле магнитные моменты атомов ориентируются преимущественно в направлении поля. Появляется намагничивание, которое усиливает внешнее поле. Однако это усиление невелико ( 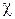мало отличается от единицы). Парамагнетиками являются кислород, платина, алюминий и др.

Механизм намагничивания, называемый диамагнетизмом, является универсальным, т.е. действует во всех веществах без исключения. Суть явления такова. Включение магнитного поля приводит к нарастанию магнитного поля в объеме вещества. Поэтому в веществе возникает индукционное электрическое поле (явление электромагнитной индукции будет рассмотрено далее). Оно воздействует на электроны, входящие в состав молекул, в результате чего движение электронов изменяется (возникают дополнительные индукционные токи). Это приводит к возникновению дополнительных магнитных моментов, причем результирующие дополнительные моменты направлены против внешнего магнитного поля, поскольку, согласно правилу Ленца, индукционные токи препятствуют изменению магнитного поля. Эти моменты должны были бы ослабить внешнее поле. Однако, этот эффект очень слаб и в чистом виде наблюдается только в диамагнетиках- веществах, в которых в отсутствие магнитного поля магнитные моменты молекул равны нулю (магнитные моменты заряженных частиц, входящих в состав молекул в сумме дают ноль). Такими веществами являются инертные газы, некоторые металлы (висмут, цинк, золото, медь и др.). На фоне ориентации во внешнем поле магнитных моментов молекул парамагнетиков он не заметен, как более слабый.

Особую группу магнитных материалов образуют ферромагнетики. Ферромагнетиками являются кристаллические тела, у которых в небольших, но макроскопических объемах - доменах (линейные размеры порядка 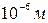) существует самопроизвольная намагниченность. Она обусловлена тем, что магнитные моменты атомов в этих объемах взаимодействуют между собой, в результате чего они ориентируются параллельно друг другу в определенном направлении. В отсутствие магнитного поля домены ориентированы хаотично и намагниченность вещества равна нулю. Во внешнем поле образец намагничивается. Это происходит двумя способами. Во-первых, домены, ориентированные вдоль поля, увеличиваются, «поглощая» домены иной ориентации. Во-вторых, магнитные моменты доменов поворачиваются, ориентируясь вдоль поля. Первый механизм преобладает в слабых, а второй – в сильных полях.

Доменное строение ферромагнетиков проявляется в магнитном гистерезисе (рис.2.10.2). При циклическом намагничивании зависимость намагниченности ферромагнетика от напряженности поля неоднозначна и нелинейна. При первичном намагничивании намагниченность растет и достигает насыщения (перестает меняться). Если затем уменьшать напряженность поля, то кривая пойдет не по первоначальному пути, а выше и при уменьшении напряженности до нуля наблюдается остаточная намагниченность. (Таким образом можно создать постоянный магнит). Для того чтобы размагнитить образец, необходимо приложить поле противоположного направления.

Из выше сказанного следует, что магнитная проницаемость ферромагнетиков не является константой. Величина магнитной проницаемости достигает очень больших значений (порядка нескольких тысяч).

При повышении температуры способность ферромагнетиков уменьшается. При некоторой температуре, называемой точкой Кюри, ферромагнитные свойства исчезают и ферромагнетик превращается в парамагнетик.