Закон полного тока для магнитного поля в веществе. Напряженность магнитного поля.
Постановка задачи. В пространство, окружающее макротоки 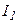 ,
, 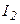 …
… 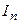 (рис. 24.2) вносим различного рода магнетики, которые в поле токов
(рис. 24.2) вносим различного рода магнетики, которые в поле токов 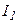 ,…
,… 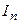 будучи намагничиваться. Найдем связь напряженности магнитного поля с токами. Предварительно свяжем намагниченность
будучи намагничиваться. Найдем связь напряженности магнитного поля с токами. Предварительно свяжем намагниченность 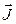 с молекулярными токами. Обозначим алгебраическую сумму макротоков
с молекулярными токами. Обозначим алгебраическую сумму макротоков  , алгебраическую сумму микротоков
, алгебраическую сумму микротоков 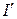 .
.
 Рассмотрим элемент контура
Рассмотрим элемент контура 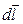 (рис. 24.3). Токи молекул справа (вне контура) не пронизывают контур. Слева (внутри контура) пронизывают контур дважды и вклад в алгебраическую сумму токов равен нулю.
(рис. 24.3). Токи молекул справа (вне контура) не пронизывают контур. Слева (внутри контура) пронизывают контур дважды и вклад в алгебраическую сумму токов равен нулю.
|
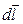 , образующий с направлением намагниченности
, образующий с направлением намагниченности 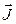 угол
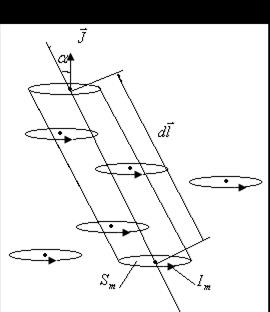
угол 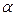 , нанизывает на себя те молекулярные токи, центры которых попадают внутрь косого цилиндра с объемом
, нанизывает на себя те молекулярные токи, центры которых попадают внутрь косого цилиндра с объемом 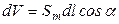 (
( 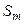 – площадь, охватываемая отдельным молекулярным током,
– площадь, охватываемая отдельным молекулярным током,  – высота косого цилиндра). Обозначим через
– высота косого цилиндра). Обозначим через 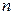 концентрацию токов
концентрацию токов 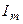 в единице объема. Сумма молекулярных токов в элементарном объеме
в единице объема. Сумма молекулярных токов в элементарном объеме 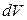 :
:
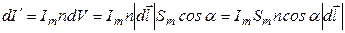 .
.
Произведение  равно магнитному моменту отдельного молекулярного тока
равно магнитному моменту отдельного молекулярного тока 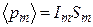 , в свою очередь
, в свою очередь 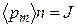 , следовательно:
, следовательно:
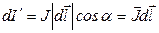 (по определению скалярного произведения). Проинтегрируем по контуру
(по определению скалярного произведения). Проинтегрируем по контуру 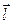 :
:
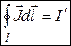
Циркуляция 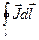 вектора
вектора 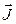 по контуру
по контуру 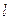 равна алгебраической сумме молекулярных токов
равна алгебраической сумме молекулярных токов 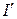 , натянутых на этот контур.
, натянутых на этот контур.
Закон полного тока с учетом токов проводимости и молекулярных токов: 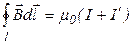 , где
, где 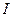 – алгебраическая сумма макротоков (знак «+» или «-» берется в соответствии с правилом правого винта по отношению к направлению обхода контура).
– алгебраическая сумма макротоков (знак «+» или «-» берется в соответствии с правилом правого винта по отношению к направлению обхода контура).
Раскроем скобки и заменим 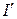 на
на 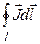 :
:
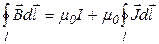
Поделив обе части на 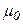 и перенося
и перенося 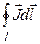 в левую часть, получим:
в левую часть, получим:
 .
.
Обозначим
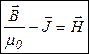
где 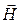 – напряженность магнитного поля. Эта величина не имеет особого физического смысла, но приносит пользу. С учетом введенного понятия напряженности получаем теорему о циркуляции вектора
– напряженность магнитного поля. Эта величина не имеет особого физического смысла, но приносит пользу. С учетом введенного понятия напряженности получаем теорему о циркуляции вектора 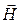 (закон полного тока для магнитного поля в веществе):
(закон полного тока для магнитного поля в веществе):
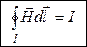
Циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макротоков, охватываемых этим контуром.
Таким образом, используя в расчетах вектор 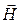 можно не учитывать молекулярные токи.
можно не учитывать молекулярные токи.
Дата добавления: 2015-08-14; просмотров: 1143;
