Энергия взаимодействия зарядов. Энергия электрического поля. Плотность энергии.
Энергия взаимодействия зарядов
Рассмотрим систему из двух точечных зарядов. Энергию взаимодействия можно трактовать как энергию первого заряда в поле второго (cм.(2.1.3))
 ,
где ,
где 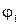 - потенциал поля, созданного вторым зарядом в точке, нахождения первого. Верно и другое утверждение: энергия взаимодействия зарядов равна энергии второго заряда в поле первого - потенциал поля, созданного вторым зарядом в точке, нахождения первого. Верно и другое утверждение: энергия взаимодействия зарядов равна энергии второго заряда в поле первого
| |
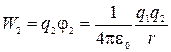 . .
|
Поскольку оба представления равноправны, энергию взаимодействия этих зарядов можно записать следующим образом
 . .
|
Таким образом, общее правило для расчета энергии взаимодействия произвольной системы точечных зарядов имеет вид
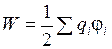 , (2.6.1 ) , (2.6.1 )
| (2.6.1 ) |
где 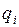 - i-тый точечный заряд системы,
- i-тый точечный заряд системы,  - потенциал поля, созданного всеми остальными зарядами системы, кроме i-того, в точке расположения заряда
- потенциал поля, созданного всеми остальными зарядами системы, кроме i-того, в точке расположения заряда 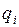 .
.
Если заряды распределены непрерывно, то, представляя систему зарядов как совокупность элементарных зарядов  и переходя к интегрированию, получим выражение
и переходя к интегрированию, получим выражение
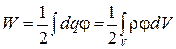 , ,
| ( 2.6.2) |
где  - объемная плотность заряда в элементарном объеме dV, а
- объемная плотность заряда в элементарном объеме dV, а 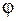 - потенциал, создаваемый всеми зарядами системы в этом объеме.
- потенциал, создаваемый всеми зарядами системы в этом объеме.
Если взаимодействуют два заряженных тела, не являющихся точечными зарядами, то нужно учитывать, что в точке, где находится заряд dq,поле создают и заряды второго тела и остальные заряды первого ( кроме выбранного dq). Тогда энергию взаимодействия этих тел можно записать
 , (2.6.3 ) , (2.6.3 )
|
где  - энергия взаимодействия друг с другом элементарных зарядов первого шарика,
- энергия взаимодействия друг с другом элементарных зарядов первого шарика,  - энергия взаимодействия друг с другом элементарных зарядов второго шарика,
- энергия взаимодействия друг с другом элементарных зарядов второго шарика,  - энергия взаимодействия элементарных зарядов первого шарика с элементарными зарядами второго шарика. Энергии
- энергия взаимодействия элементарных зарядов первого шарика с элементарными зарядами второго шарика. Энергии  и
и  называют собственными энергиями зарядов
называют собственными энергиями зарядов  и
и 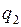 . Энергию
. Энергию  называют энергией взаимодействия зарядов
называют энергией взаимодействия зарядов  и
и 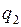 .
.
Энергия уединенного проводника и конденсатора
Пусть проводник имеет заряд 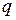 и потенциал
и потенциал 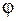 . Энергия проводника
. Энергия проводника 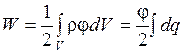 . Поскольку проводник является эквипотенциальной областью, то потенциал выносится из-под знака интеграла. Окончательно
. Поскольку проводник является эквипотенциальной областью, то потенциал выносится из-под знака интеграла. Окончательно
 . ( 2.6.4 ) . ( 2.6.4 )
|
Или с учетом формулы для электроемкости проводника
 . ( 2.6.5 ) . ( 2.6.5 )
| (2.24) |
Энергия конденсатора.
Пусть 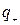 и
и  - заряд и потенциал положительно заряженной обкладки, а
- заряд и потенциал положительно заряженной обкладки, а 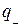 и
и 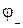 - соответственно отрицательной. Тогда энергия конденсатора с учетом
- соответственно отрицательной. Тогда энергия конденсатора с учетом 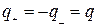 и
и  запишется
запишется
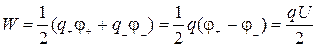 . .
| (2.6.6 ) |
Здесь учтено, что по модулю заряды равны. Воспользуемся формулой для электроемкости и получим для энергии конденсатора еще две формулы.
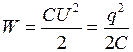 . .
| (2.6.7 ) |
Энергия электрического поля.
Физический смысл энергии конденсатора это не что иное, как энергия электрического поля сосредоточенного внутри него. Получим выражение для энергии плоского конденсатора через напряженность. Будем пренебрегать краевыми эффектами. Воспользуемся формулой 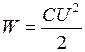 , и выражением для емкости плоского конденсатора
, и выражением для емкости плоского конденсатора  .
.
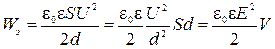 , ,
|
Здесь мы воспользовались соотношениями  (для напряженности поля в конденсаторе) и
(для напряженности поля в конденсаторе) и 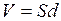 (объем области между обкладками конденсатора). В случае если диэлектрик изотропный, можем с учетом формулы (2.5.8) перейти к общей формуле
(объем области между обкладками конденсатора). В случае если диэлектрик изотропный, можем с учетом формулы (2.5.8) перейти к общей формуле
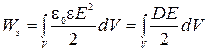 . .
| (2.6.8) |
Подынтегральное выражение здесь имеет смысл энергии, заключенной в объеме. Это подводит к важной идее о локализации энергии в самом поле.
Это предположение находит подтверждение в области переменных полей. Именно переменные поля могут существовать независимо от возбудивших их электрических зарядов и распространяться в пространстве в виде электромагнитных волн, которые переносят энергию.
Таким образом, носителем энергии является само поле.
Анализируя последнее выражение, можем ввести объемную плотность энергии, т.е. энергии, заключенной в единице объема
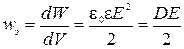 . .
| (2.6.9) |
Мы получили (2.6.8) и (2.6.9) в частном случае однородного, изотропного диэлектрика в однородном электрическом поле. В этом случае векторы  и
и  сонаправлены и можно записать
сонаправлены и можно записать
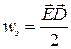 . ( 2.6.10 )
. ( 2.6.10 )
Однако нужно отметить, что соотношение (2.6.10) справедливо и в других случаях.
Дата добавления: 2015-08-08; просмотров: 1136;
