Электроемкость. Конденсаторы.

Электроемкость уединенного проводника.

Если сообщить уединенному проводнику заряд q, он создаст в окружающем пространстве электрическое поле и потенциал проводника будет равен , причем потенциал пропорционален заряду. При изменении заряда соответствующим образом изменится и потенциал. Поэтому можно ввести коэффициент пропорциональности между q и . Этот коэффициент называется электроемкостью уединенного проводника(сокращенно емкость).

С= 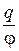. ( 2.4.3 )

Поскольку потенциал заряда пропорционален его величине, то их отношение не зависит ни от 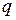, ни от 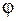, а, зависит очевидно от распределения заряда по поверхности проводника (другими словами от его формы и размеров).

Если вблизи проводника будут находиться другие тела, то поле, созданное зарядом проводника приведет к перераспределению зарядов в этих телах, что изменит структуру поля, а следовательно и потенциал проводника. Таким образом, коэффициент пропорциональности между потенциалом и зарядом изменится. Поэтому говорят об уединенном проводнике.

В качестве примера рассчитаем емкость уединенного проводника, имеющего форму шара радиуса 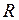, Пусть шару сообщен заряд 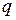. Заряд будет равномерно распределен по поверхности шара. Напряженность поля внутри равна нулю. Поле снаружи (см.2.3.3)

.

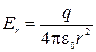Рассчитаем потенциал шара, полагая потенциал равным нулю на бесконечности

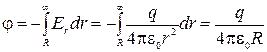. ( 2.4.4 )

Тогда из (2.4.3) следует

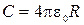. ( 2.4.5 )

Таким образом, электроемкость уединенного проводника зависит от его формы, размеров и, как будет ясно впоследствии, от свойств окружающей среды (диэлектрической проницаемости среды).

Единицей электроемкости в системе СИ является фарада (Ф).

Чтобы внешние тела не влияли на электроемкость необходимо создать систему проводников такую, чтобы находящиеся на них заряды создавали поле в ограниченной области пространства. Такая система называется конденсатором. Простейший конденсатор состоит из двух проводников (обкладок), расположенных на малом расстоянии друг от друга, заряженных равными по модулю, разноименными зарядами.

Чтобы внешние тела не оказывали влияние на емкость конденсатора, его обкладки располагают так относительно друг друга, чтобы поле, создаваемое зарядами обкладок, было сосредоточено практически полностью между ними. Емкостью конденсатораявляется отношение модуля заряда обкладки к разности потенциалов между обкладками (напряжением U).

.

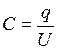( 2.4.6 )

Емкость конденсатора также зависит только от его размеров и формы. Самым простым конденсатором является плоский конденсатор. Его обкладки представляют собой плоские пластины площади S, расположенные на расстоянии d много меньшем их размеров. В этом случае для области между пластинами их можно полагать бесконечными (искажением поля вблизи краев пренебрегают). Рассчитаем его емкость.

Пусть на одной обкладке находится заряд q, а на другой -q . Поскольку пластины полагаем бесконечными, то модуль напряженности поля, создаваемого каждой пластиной одинаков и определен соотношением (2.3.6). Поэтому как видно из рис.2.4.5 результирующая напряженность вне конденсатора равна нулю, а между пластинами

Е= 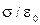, где поверхностная плотность заряда 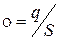. Тогда найдем разность потенциалов между обкладками (ось х перпендикулярна обкладкам)

.

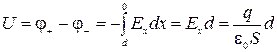Тогда из (2.4.6) следует

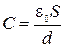. ( 2.4.7 )

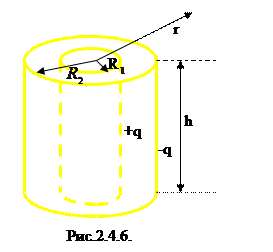
Найдем еще электроемкость цилиндрического конденсатора, который представляет собой два коаксиальных цилиндра радиусами R 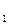и 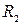и высотой h (рис 2.4.6). Напряженность поля между обкладками создается только внутренним цилиндром и равна (см.2.3.5а )

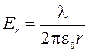, где заряд на единицу длины цилиндра 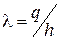. Тогда разность потенциалов между обкладками

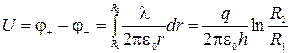
и электроемкость цилиндрического конденсатора

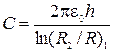. ( 2.4.8 )

Таким образом, емкость конденсатора (как и уединенного проводника) зависит от его формы, размеров и диэлектрической проницаемости среды между обкладками.