Условия существования электрического тока. Сила тока, плотность тока.
Электрическим током называется упорядоченное движение заряженных частиц. Следовательно, электрический ток может существовать только в среде, где возможно перемещение заряженных частиц, т.е. в проводниках. Эти частицы называют носителями тока. При отсутствии электрического поля носители заряда в среде совершают тепловое хаотическое движение. При включении электрического поля наряду с хаотическим движением наблюдается упорядоченное движение с некоторой средней скоростью и через любую воображаемую поверхность S появится ток. Количественной мерой электрического тока служит сила тока I .
Сила тока равна заряду, переносимому через рассматриваемую поверхность за единицу времени 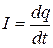 . (2.6.11 ) . (2.6.11 )
|
В системе Си единицей силы тока является ампер (А). Если сила тока не меняется с течением времени, ток называется постоянным.
Густота зарядов, пересекающих поверхность, может быть различной в разных точках. Поэтому для более детальной характеристики тока вводят вектор плотности тока 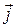 . Плотностью токаназывается вектор, направленный в сторону движения положительного заряда и численно равный отношению силы тока через единичную площадку, перпендикулярную движению заряженных частиц, к величине этой площадки.
. Плотностью токаназывается вектор, направленный в сторону движения положительного заряда и численно равный отношению силы тока через единичную площадку, перпендикулярную движению заряженных частиц, к величине этой площадки.
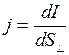 . .
| (2.6.12) |
За направление этого вектора принимают направление скорости упорядоченного движения положительных носителей. Поле вектора 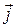 можно изобразить графически с помощью линий тока, которые проводят аналогично линиям вектора можно изобразить графически с помощью линий тока, которые проводят аналогично линиям вектора  . .
|
Зная вектор плотности тока в каждой точке площадки, можно найти силу тока через эту площадку
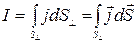 . .
| (2.6.12) |
Из (2.6.12) видно, что сила тока является величиной скалярной и алгебраической. Ее знак определяется выбором направления нормали к поверхности S.
Рассмотрим в проводящей среде, где течет ток, замкнутую поверхность. Тогда интеграл 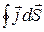 определяет заряд, выходящий (или входящий) за единицу времени из объема V,ограниченного поверхностью S. Из закона сохранения заряда этот интеграл равен убыли заряда в единицу времени внутри объема V
определяет заряд, выходящий (или входящий) за единицу времени из объема V,ограниченного поверхностью S. Из закона сохранения заряда этот интеграл равен убыли заряда в единицу времени внутри объема V
 . .
| (2.6.13) |
Это соотношение называют уравнением непрерывности. Если ток постоянный, то распределение заряда в пространстве должно оставаться неизменным, то есть 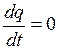 . Следовательно
. Следовательно
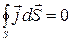 . .
| (2.6.14) |
Линии вектора 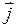 при этом нигде не начинаются и не заканчиваются (являются замкнутыми). Другими словами, поле вектора
при этом нигде не начинаются и не заканчиваются (являются замкнутыми). Другими словами, поле вектора 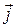 в таком случае не имеет источников.
в таком случае не имеет источников.
Сторонние силы. Электродвижущая сила. Напряжение.
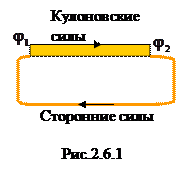 Пусть на концах проводника создана разность потенциалов (для определенности
Пусть на концах проводника создана разность потенциалов (для определенности 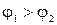 ). Тогда кулоновские силы будут перемещать положительные носители от большего потенциала к меньшему – потечет электрический ток. Этот процесс приведет к перераспределению зарядов, в результате чего электрическое поле в проводнике пропадет и электрический ток прекратится. Чтобы в проводнике тек постоянный ток, необходимо поддерживать разность потенциалов на его концах. Для этого необходимы силы, которые перемещали бы заряды от меньшего потенциала к большему. Эти силы называют сторонними. Сторонние силы, как и кулоновские, можно характеризовать работой, которую они совершают, перемещая заряды. Работа, которую совершают сторонние силы при перемещении единичного положительного заряда, называется электродвижущей силой (э,д,с, - Є).
). Тогда кулоновские силы будут перемещать положительные носители от большего потенциала к меньшему – потечет электрический ток. Этот процесс приведет к перераспределению зарядов, в результате чего электрическое поле в проводнике пропадет и электрический ток прекратится. Чтобы в проводнике тек постоянный ток, необходимо поддерживать разность потенциалов на его концах. Для этого необходимы силы, которые перемещали бы заряды от меньшего потенциала к большему. Эти силы называют сторонними. Сторонние силы, как и кулоновские, можно характеризовать работой, которую они совершают, перемещая заряды. Работа, которую совершают сторонние силы при перемещении единичного положительного заряда, называется электродвижущей силой (э,д,с, - Є).
Є  =
= 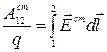 , ( 2.6.15 )
, ( 2.6.15 )
где 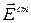 - напряженность поля сторонних сил, которая направлена отменьшего потенциала к большему. Как видно из определения э.д.с. измеряется в вольтах (В).
- напряженность поля сторонних сил, которая направлена отменьшего потенциала к большему. Как видно из определения э.д.с. измеряется в вольтах (В).
Поскольку работу при перемещении зарядов в проводнике совершают и кулоновские, и сторонние силы, то можно ввести величину равную работе всех сил по перемещению единичного положительного заряда в проводнике. Эту величину называют падением напряжения (или просто напряжением)-U
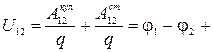 Є
Є 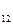 . ( 2.6.16 )
. ( 2.6.16 )
Если рассматривать замкнутую цепь, по которой течет постоянный ток, то суммарная работа всех сил по перемещению заряда, отлична от нуля. А поскольку работа кулоновских сил в этом случае равна нулю, то отличной от нуля должна быть работа сторонних сил, т.е.
Є=  . (2.6.17 )
. (2.6.17 )
Таким образом, поле сторонних сил не является потенциальным.
Закон Ома. Правила Кирхгофа.
Закон Ома в интегральной форме. Электрическое сопротивление.
Открытый экспериментально закон Ома гласит: сила тока, протекающего по проводнику, пропорциональна напряжению на его концах
I= 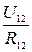 . ( 2.7.1 )
. ( 2.7.1 )
Здесь 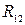 - характеристика проводника, называемая электрическим сопротивлением. Сопротивление зависит от формы и размеров проводника, от его материала и температуры (в общем случае еще и от распределения тока по проводнику). В простейшем случае однородного цилиндрического проводника
- характеристика проводника, называемая электрическим сопротивлением. Сопротивление зависит от формы и размеров проводника, от его материала и температуры (в общем случае еще и от распределения тока по проводнику). В простейшем случае однородного цилиндрического проводника 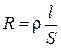 , ( 2.7.2 )
, ( 2.7.2 )
где l - длина проводника, S - площадь его поперечного сечения,  - удельное электрическое сопротивление, зависящее от материала проводника и его температуры. Единицей измерения сопротивления в системе СИ является ом (Ом), а удельного сопротивления ом-метр (Ом∙м).
- удельное электрическое сопротивление, зависящее от материала проводника и его температуры. Единицей измерения сопротивления в системе СИ является ом (Ом), а удельного сопротивления ом-метр (Ом∙м).
Если учесть соотношения (2.7.1) и (2.6.16), то закон Ома для участка цепи можно записать
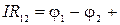 Є
Є 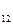 . ( 2.7.3 )
. ( 2.7.3 )
Необходимо помнить, что э.д.с., как и сила тока, величина алгебраическая. Поэтому, когда сторонние силы способствуют движению положительных носителей в выбранном направлении (от точки 1 к точке 2), э.д.с. положительна, в противном случае отрицательна.
В частном случае однородного участка цепи (отсутствуют сторонние силы) напряжение и разность потенциалов совпадают.
Положив 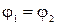 , получим закон Ома для замкнутой цепи
, получим закон Ома для замкнутой цепи
I=Є/R  . ( 2.7.4 )
. ( 2.7.4 )
Здесь Є – э.д.с., действующая в цепи, R  - полное сопротивление всей цепи, включающее в себя внешнее сопротивление – сопротивление нагрузки (R) и внутреннее сопротивление источника (участка, где действуют сторонние силы) – r R
- полное сопротивление всей цепи, включающее в себя внешнее сопротивление – сопротивление нагрузки (R) и внутреннее сопротивление источника (участка, где действуют сторонние силы) – r R  =R+r.
=R+r.
Закон Ома в дифференциальной форме.
 Получим этот закон в дифференциальной форме. Рассмотрим случай изотропного проводника, в котором направления векторов
Получим этот закон в дифференциальной форме. Рассмотрим случай изотропного проводника, в котором направления векторов 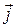 и
и  совпадают. Мысленно в проводящей среде выделим элементарный цилиндрический объем как показано на рис. 2.7.1. Для такого проводника запишем формулу (2.7.4) в следующем виде
совпадают. Мысленно в проводящей среде выделим элементарный цилиндрический объем как показано на рис. 2.7.1. Для такого проводника запишем формулу (2.7.4) в следующем виде
 .
.
После преобразований получим в векторном виде выражение
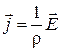 , ( 2.7.5 )
которое выражает закон Ома в дифференциальной форме. Оно устанавливает связь между величинами, относящимися к одной и той же точке проводника.
Электрическое поле проводника с током.
При протекании постоянного тока по проводнику избыточного заряда внутри однородного проводника нет. В самом деле, из (2.6.14) и (2.7.5) при условии, что интеграл взят по произвольной замкнутой поверхности внутри проводника и постоянную величину , ( 2.7.5 )
которое выражает закон Ома в дифференциальной форме. Оно устанавливает связь между величинами, относящимися к одной и той же точке проводника.
Электрическое поле проводника с током.
При протекании постоянного тока по проводнику избыточного заряда внутри однородного проводника нет. В самом деле, из (2.6.14) и (2.7.5) при условии, что интеграл взят по произвольной замкнутой поверхности внутри проводника и постоянную величину  можно вынести из-под интеграла, будем иметь можно вынести из-под интеграла, будем иметь
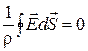 .
Тогда из теоремы Гаусса следует, что заряд внутри поверхности (всюду внутри проводника) равен нулю. Избыточный заряд может появиться только на поверхности проводника, в местах соприкосновения с другими проводниками, где проводник имеет неоднородности. .
Тогда из теоремы Гаусса следует, что заряд внутри поверхности (всюду внутри проводника) равен нулю. Избыточный заряд может появиться только на поверхности проводника, в местах соприкосновения с другими проводниками, где проводник имеет неоднородности.
 Отсюда следует, что снаружи проводника имеется нормальная составляющая вектора Отсюда следует, что снаружи проводника имеется нормальная составляющая вектора 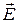 (Е (Е 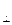 ). Из непрерывности тангенциальной составляющей вектора ). Из непрерывности тангенциальной составляющей вектора 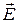 на границе раздела сред следует, что вблизи поверхности существует и тангенциальная составляющая на границе раздела сред следует, что вблизи поверхности существует и тангенциальная составляющая 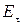 (поскольку существует поле внутри) Электрическое поле проводника с током имеет вид, показанный на рис. 2.7.2.
Внутри проводника электрическое поле не равно нулю. Однако, распределение зарядов внутри проводника не меняется во времени, хотя они движутся (в каждой точке на место уходящих зарядов приходят новые). Таким образом, эти заряды создают внутри проводника такое же кулоновское потенциальное поле, но оно отличается от поля стационарных зарядов и потому не равно нулю.
Правила Кирхгоффа
На основании законов Ома, закона сохранения заряда и уравнения непрерывности сформулированы правила расчета сложных цепей. Их два.
Первое правило Кирхгофа формулируется для узлов электрической цепи. Узломназывается электрический контакт трех и более проводов. Из закона сохранения заряда и непрерывности линий тока следует: алгебраическая сумма токов втекающих и вытекающих из узла равна нулю. (поскольку существует поле внутри) Электрическое поле проводника с током имеет вид, показанный на рис. 2.7.2.
Внутри проводника электрическое поле не равно нулю. Однако, распределение зарядов внутри проводника не меняется во времени, хотя они движутся (в каждой точке на место уходящих зарядов приходят новые). Таким образом, эти заряды создают внутри проводника такое же кулоновское потенциальное поле, но оно отличается от поля стационарных зарядов и потому не равно нулю.
Правила Кирхгоффа
На основании законов Ома, закона сохранения заряда и уравнения непрерывности сформулированы правила расчета сложных цепей. Их два.
Первое правило Кирхгофа формулируется для узлов электрической цепи. Узломназывается электрический контакт трех и более проводов. Из закона сохранения заряда и непрерывности линий тока следует: алгебраическая сумма токов втекающих и вытекающих из узла равна нулю.
 Токи, притекающие к узлу, берут со знаком плюс, токи, вытекающие из узла, – со знаком минус. Для узла на рис. 2.7.3 запишем первое правило Кирхгофа Токи, притекающие к узлу, берут со знаком плюс, токи, вытекающие из узла, – со знаком минус. Для узла на рис. 2.7.3 запишем первое правило Кирхгофа 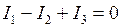 .
Если в цепи N узлов, то первое правило пишут для ( .
Если в цепи N узлов, то первое правило пишут для ( 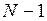 ) узла.
Направление тока на отдельных участках разветвленной цепи расставляется произвольно. Следует помнить, что при последовательном соединении ток через поперечное сечение проводника всюду одинаковый. Это означает, что на участке цепи от узла до узла ток имеет одно и тоже значение.
Второе правило Кирхгофаформулируется для замкнутых контуров, на которые разбивается сложная цепь. Контуры не должны повторять друг друга. Из законов Ома следует, что алгебраическая сумма падений напряжения на замкнутом контуре равна алгебраической сумме ЭДС, включенных в этот контур. ) узла.
Направление тока на отдельных участках разветвленной цепи расставляется произвольно. Следует помнить, что при последовательном соединении ток через поперечное сечение проводника всюду одинаковый. Это означает, что на участке цепи от узла до узла ток имеет одно и тоже значение.
Второе правило Кирхгофаформулируется для замкнутых контуров, на которые разбивается сложная цепь. Контуры не должны повторять друг друга. Из законов Ома следует, что алгебраическая сумма падений напряжения на замкнутом контуре равна алгебраической сумме ЭДС, включенных в этот контур.
В качестве примера используем эти правила для расчета токов и цепи, приведенной на рис.2.7.4.
Далее решается эта система уравнений.
Работа электрического тока. Закон Джоуля – Ленца. При протекании тока по замкнутой цепи отличную от нуля работу совершают только сторонние силы, действующие только внутри источника
C учетом определений силы тока (2.6.11) и закона Ома для замкнутой цепи (2.7.4) получим
Полученное выражение можно интерпретировать следующим образом: первое слагаемое представляет собой работу, совершаемую при протекании тока по внешней цепи (в нагрузке), а второе, соответственно, внутри источника. За счет этой работы изменяется некоторая энергия. Если проводник неподвижен и в нем не происходят химические превращения, то эта энергия должна выделяться в форме внутренней (тепловой) энергии. Механизм этого превращения таков: под воздействием электрического поля электроны ускоряются и приобретают дополнительную кинетическую энергию. При столкновении с ионами в узлах кристаллической решетки электроны отдают им эту энергию. Колебания ионов усиливаются, что приводит к увеличению внутренней энергии вещества и повышению его температуры. Таким обра-зом, при протекании тока в нагрузке выделяется количество тепла
Эта формула выражает закон Джоуля – Ленца, а величина
тепловую мощность, выделяющуюся на внешней цепи. Величина I
|
Дата добавления: 2015-08-08; просмотров: 1019;

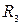

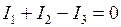
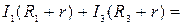 Є
Є  ─Є
─Є 
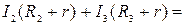 Є
Є  ─Є
─Є 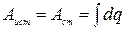 Є. ( 2.7.6 )
Є. ( 2.7.6 )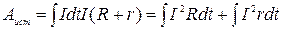 . (2.7.7 )
. (2.7.7 )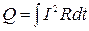 . ( 2.7.8 )
. ( 2.7.8 )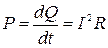 =
= 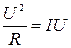 ( 2.7.9 )
( 2.7.9 ) r является мощностью, выделяющейся внутри источника, т.е. потерянной энергией. Следовательно, можно говорить о коэффициенте полезного действия электрической цепи
r является мощностью, выделяющейся внутри источника, т.е. потерянной энергией. Следовательно, можно говорить о коэффициенте полезного действия электрической цепи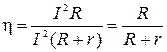 ( 2.7.10)
( 2.7.10)