Магнитное поле , его силовая характеристика.Закн Био – Савара – Лапласа.
Сила Лоренца. Магнитное поле в вакууме.
Как уже было отмечено, характер взаимодействия электрических зарядов зависит от состояния их движения. Свойства поля, создаваемого зарядами, также зависят от характера их движения.
Поле, создаваемое движущимися зарядами (или токами), называется магнитным. Как и любое поле, оно имеет силовую характеристику – величину, которая определяет силу, с которой поле действует на заряды. Силовая характеристика магнитного поля называется вектор магнитной индукции. Принято обозначать ее  . Единицей магнитной индукции является тесла (Тл).
. Единицей магнитной индукции является тесла (Тл).
Как показывает опыт, магнитное поле действует только на движущиеся относительно него заряды, и величина силы зависит от скорости заряда. Кроме того сила должна зависеть от самого заряда и силовой характеристики поля. Тогда по аналогии с силой, действующей на неподвижный заряд в электрическом поле можно записать, что сила определяется векторным произведением скорости заряда и силовой характеристики поля
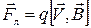 ( 2.8.1 )
( 2.8.1 )
Эта сила называется силой Лоренца.
(Часто силой Лоренца называют силу, с которой действуют на заряд и электрическое и магнитное поле 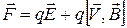 . Здесь нужно заметить, что в нерелятивистском приближении обобщенная сила Лоренца не зависит от выбора инерциальной системы отсчета. Однако, в общем случае магнитная составляющая силы Лоренца меняется при переходе от одной системы отсчета к другой из-за скорости. Поэтому должна меняться и электрическая составляющая. Отсюда следует, что разделение полной силы на электрическую и магнитную зависит от выбора системы отсчета.)
. Здесь нужно заметить, что в нерелятивистском приближении обобщенная сила Лоренца не зависит от выбора инерциальной системы отсчета. Однако, в общем случае магнитная составляющая силы Лоренца меняется при переходе от одной системы отсчета к другой из-за скорости. Поэтому должна меняться и электрическая составляющая. Отсюда следует, что разделение полной силы на электрическую и магнитную зависит от выбора системы отсчета.)
Из (2.8.1) видно, что сила Лоренца всегда перпендикулярна скорости заряда, а следовательно не совершает работы над зарядом и потому не изменяет кинетическую энергию заряда.
Индукция магнитного поля движущегося точечного заряда.
Индукция магнитного поля движущегося точечного заряда должна зависеть от скорости заряда, а также от величины самого заряда и положения точки, в которой нужно определить вектор индукции. Тогда по аналогии с силовой характеристикой электрического поля точечного заряда (2.2.1) можно записать
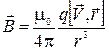 , ( 2.8.2 ) , ( 2.8.2 )
| (2.8.2 |
где 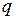 - величина точечного заряда, вокруг которого возникает магнитное поле,
- величина точечного заряда, вокруг которого возникает магнитное поле, 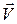 - вектор скорости данного заряда,
- вектор скорости данного заряда, 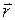 - радиус-вектор, проведенный от заряда в точку, где рассчитываем индукцию магнитного поля. Коэффициент
- радиус-вектор, проведенный от заряда в точку, где рассчитываем индукцию магнитного поля. Коэффициент 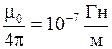 обусловлен выбором системы единиц СИ, константа
обусловлен выбором системы единиц СИ, константа 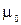 называется магнитной постоянной. Как видно из (2.8.2) вектор магнитной индукции всегда перпендикулярен скорости заряда и радиус-вектору данной точки.
называется магнитной постоянной. Как видно из (2.8.2) вектор магнитной индукции всегда перпендикулярен скорости заряда и радиус-вектору данной точки.
Индукция магнитного поля тока. Закон Био – Савара – Лапласа.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитное поле, создаваемое несколькими движущимися зарядами (или токами), равно векторной сумме магнитных полей, создаваемых каждым зарядом (или током) в отдельности
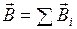 .
Если воспользоваться этим принципом и учесть формулу (2.8.2), то можно получить выражение для расчета индукции магнитного поля, созданного элементом линейного тока, которое носит название закона Био – Савара – Лапласа (или Био – Савара) .
Если воспользоваться этим принципом и учесть формулу (2.8.2), то можно получить выражение для расчета индукции магнитного поля, созданного элементом линейного тока, которое носит название закона Био – Савара – Лапласа (или Био – Савара)
| |||
d 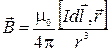 . (2.8.3 ) . (2.8.3 )
| |||
Если ток течет по тонкому проводу, то бывает удобно ввести линейный элемент тока 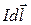 , где
, где 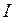 - сила тока, протекающего по элементу провода длиной dl, а направление вектора
- сила тока, протекающего по элементу провода длиной dl, а направление вектора 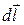 совпадает с направлением тока. Вектор
совпадает с направлением тока. Вектор 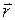 проводят от элемента тока к точке, в которой рассчитывают индукцию магнитного поля. Для линейного проводника произвольной формы и конечных размеров полное поле согласно принципу суперпозиции определяется в результате интегрирования выражения (2.8.3) по всем элементам тока
проводят от элемента тока к точке, в которой рассчитывают индукцию магнитного поля. Для линейного проводника произвольной формы и конечных размеров полное поле согласно принципу суперпозиции определяется в результате интегрирования выражения (2.8.3) по всем элементам тока
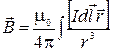 . ( 2.8.4 )
. ( 2.8.4 )
Рассмотрим несколько примеров.
1.Поле прямого тока.
Рассчитаем поле участка прямого провода длиной 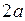 , по которому течет ток
, по которому течет ток 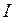 , в точке, удаленной на расстояние
, в точке, удаленной на расстояние 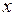 по оси, проведенной перпендикулярно проводу через его середину.
по оси, проведенной перпендикулярно проводу через его середину.
 Выделим элемент с током
Выделим элемент с током 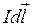 . Вектор
. Вектор 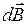 от такого элемента указан на рис. 2.8.1. В ту же сторону будет направлен вектор
от такого элемента указан на рис. 2.8.1. В ту же сторону будет направлен вектор 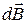 от любого другого элемента тока. Следовательно, и результирующий вектор
от любого другого элемента тока. Следовательно, и результирующий вектор 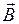 будет сонаправлен вектору
будет сонаправлен вектору 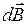 . Поэтому находим модуль вектора магнитной индукции, суммируя модули векторов
. Поэтому находим модуль вектора магнитной индукции, суммируя модули векторов 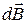 .
.
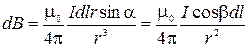 .
.
Переменные 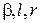 связаны
связаны
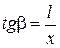 .
.
Дифференцируя последнее выражение, получим:
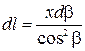 . .
| (2.8.5) |
Также воспользуемся соотношением:
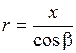 . .
| (2.8.6) |
С учетом (2.8.5) и (2.8.6) получим интеграл для расчета поля
 = =  .
Угол .
Угол 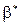 это максимальное значение угла это максимальное значение угла 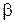 . .
|
Учтем, что 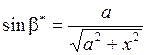 . После несложных преобразований получим окончательное выражение
. После несложных преобразований получим окончательное выражение
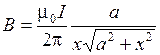 . .
| (2.8.7) |
Для случая x«a (переход к бесконечно длинному прямому проводнику) получим 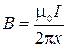 . ( 2.8.8 )
. ( 2.8.8 )
2.Магнитное поле на оси кругового тока
На рис 2.8.2 а показано направление индукции поля кольцевого тока на расстоянии 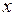 от центра по оси, проведенной перпендикулярно плоскости кольца. Вектор
от центра по оси, проведенной перпендикулярно плоскости кольца. Вектор 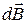 от элемента тока, расположенного в начале изображенного радиус-вектора
от элемента тока, расположенного в начале изображенного радиус-вектора 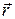 показан на рисунке. Очевидно, что векторы
показан на рисунке. Очевидно, что векторы 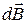 от других элементов тока будут направлены по образующим конуса с углом полураствора
от других элементов тока будут направлены по образующим конуса с углом полураствора 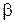 . Следовательно, результирующий вектор магнитной индукции будет направлен по оси х и для его расчета необходимо сложить проекции векторов
. Следовательно, результирующий вектор магнитной индукции будет направлен по оси х и для его расчета необходимо сложить проекции векторов 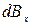 на эту ось.
на эту ось.
 Согласно закону Био-Савара можно записать
Согласно закону Био-Савара можно записать
 . .
|
Применим принцип суперпозиции
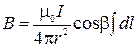 . .
|
Воспользовавшись геометрическими соотношениями: 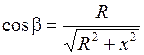 ,
, 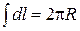 , получим
, получим
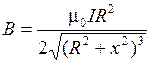 . (2.8.9) . (2.8.9)
|
На рис. 2.8.2 б показано направление вектора 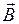 кругового тока в центре кольца. Из соотношения (2.8.9), если
кругового тока в центре кольца. Из соотношения (2.8.9), если  получим выражение для модуля вектора индукции магнитного поля в центре кругового тока.
получим выражение для модуля вектора индукции магнитного поля в центре кругового тока.
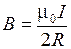 . (2.8.10)
Лекция 2.9.
Поток и циркуляция вектора . (2.8.10)
Лекция 2.9.
Поток и циркуляция вектора  . Контур с током в магнитном поле.
Теорема Гаусса для вектора . Контур с током в магнитном поле.
Теорема Гаусса для вектора  . .
|
Как и любое другое векторное поле, магнитное поле может быть представлено силовыми линиями – линиями вектора  . Их проводят так, чтобы касательная к ним в каждой точке совпадала с направлением вектора
. Их проводят так, чтобы касательная к ним в каждой точке совпадала с направлением вектора  , а густота линий пропорциональна его модулю. Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора
, а густота линий пропорциональна его модулю. Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора  не имеют ни начала, ни конца. Поэтому поток вектора
не имеют ни начала, ни конца. Поэтому поток вектора  через замкнутую поверхность должен быть равен нулю
через замкнутую поверхность должен быть равен нулю
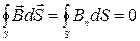 . ( 2.9.1 )
. ( 2.9.1 )
Эта формула выражает теорему Гаусса для вектора  . Это означает, что число линий магнитной индукции, выходящих из любого объема, ограниченного замкнутой поверхностью, всегда равно числу линий, входящих в этот объем. Отсюда следует, что поток вектора
. Это означает, что число линий магнитной индукции, выходящих из любого объема, ограниченного замкнутой поверхностью, всегда равно числу линий, входящих в этот объем. Отсюда следует, что поток вектора  через поверхность, ограниченную некоторым замкнутым контуром, не зависит от формы поверхности.
через поверхность, ограниченную некоторым замкнутым контуром, не зависит от формы поверхности.
Теорема о циркуляции вектора  .
.
 Рассчитаем циркуляцию
Рассчитаем циркуляцию  в простейшем случае, когда поле создается прямым бесконечно длинным проводником. Пусть замкнутый контур лежит в плоскости, перпендикулярной проводнику. Ток направлен за чертеж (рис. 2.9.1). В каждой точке контура
в простейшем случае, когда поле создается прямым бесконечно длинным проводником. Пусть замкнутый контур лежит в плоскости, перпендикулярной проводнику. Ток направлен за чертеж (рис. 2.9.1). В каждой точке контура  направлен по касательной к окружности, центр которой совпадает с током, а его модуль рассчитывается по формуле (2.8.8). Для расчета заметим, что
направлен по касательной к окружности, центр которой совпадает с током, а его модуль рассчитывается по формуле (2.8.8). Для расчета заметим, что 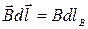 , где
, где 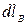 - проекция элемента контура на направление вектора
- проекция элемента контура на направление вектора  (
( 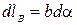 ). С учетом выше сказанного
). С учетом выше сказанного
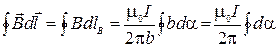 .
.
При обходе по контуру, охватывающему ток, радиальная прямая поворачивается в одном направлении и 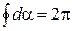 . Если ток не охватывается контуром, то этот интеграл равен нулю. Если направление тока противоположно указанному на рисунке, то
. Если ток не охватывается контуром, то этот интеграл равен нулю. Если направление тока противоположно указанному на рисунке, то 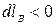 . Обобщая все сказанное, делаем вывод
. Обобщая все сказанное, делаем вывод
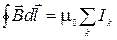 , ( 2.9.2 )
, ( 2.9.2 )
где в правой части стоит алгебраическая сумма токов, охватываемых контуром. Со знаком плюс учитываются токи, направление которых с направлением обхода по контуру связано правилом правого винта. С учетом формулы (2.6.12) запишем 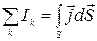 . Интеграл берется по произвольной поверхности, опирающейся на контур. Тогда окончательно
. Интеграл берется по произвольной поверхности, опирающейся на контур. Тогда окончательно
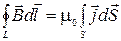 . (2.9.3 )
. (2.9.3 )
В левой части уравнения берется интеграл по произвольному замкнутому контуру, в правой – по поверхности, опирающейся на этот контур. Направление обхода и направление нормали к поверхности связаны правилом правого винта.
Таким образом, из формул (2.9.2) или (2.9.3) следует, что магнитное поле не является потенциальным.
Теорема о циркуляции вектора  позволяет в ряде случаев рассчитать индукцию магнитного поля (обычно в случае высокой симметрии задачи). Рассмотрим примеры.
позволяет в ряде случаев рассчитать индукцию магнитного поля (обычно в случае высокой симметрии задачи). Рассмотрим примеры.
Рассчитаем индукцию магнитного поля длинного тонкого соленоида. Пусть ток 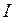 течет по проводнику, намотанному по винтовой линии на поверхность цилиндра. Такой обтекаемый током цилиндр называют соленоидом. Пусть на единицу длины соленоида приходится
течет по проводнику, намотанному по винтовой линии на поверхность цилиндра. Такой обтекаемый током цилиндр называют соленоидом. Пусть на единицу длины соленоида приходится 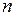 витков проводника. Шаг винтовой линии достаточно мал, и каждый виток провода можно считать замкнутым витком. Сечение провода также мало, ток соленоида можно считать текущим по его поверхности. Чем длиннее соленоид, тем меньше индукция магнитного поля снаружи него, а для бесконечно длинного соленоида магнитное поле снаружи и вовсе отсутствует. Из соображений симметрии следует, что линии вектора
витков проводника. Шаг винтовой линии достаточно мал, и каждый виток провода можно считать замкнутым витком. Сечение провода также мало, ток соленоида можно считать текущим по его поверхности. Чем длиннее соленоид, тем меньше индукция магнитного поля снаружи него, а для бесконечно длинного соленоида магнитное поле снаружи и вовсе отсутствует. Из соображений симметрии следует, что линии вектора 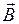 направлены вдоль оси внутри соленоида и образуют правовинтовую систему с направлением тока. Выберем контур как показано на рис.2.9.2.
направлены вдоль оси внутри соленоида и образуют правовинтовую систему с направлением тока. Выберем контур как показано на рис.2.9.2.
 При расчете циркуляции
При расчете циркуляции  разобьем интеграл по замкнутому контуру на четыре интеграла по сторонам прямоугольника. Интегралы по сторонам перпендикулярным образующей цилиндра и по стороне, расположенной вне соленоида будут равны нулю и поэтому
разобьем интеграл по замкнутому контуру на четыре интеграла по сторонам прямоугольника. Интегралы по сторонам перпендикулярным образующей цилиндра и по стороне, расположенной вне соленоида будут равны нулю и поэтому 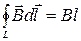 .
.
Здесь l - длина стороны контура внутри соленоида. Число витков провода, пронизывающих любую поверхность, опирающуюся на выбранный контур равно nl. Тогда по теореме о циркуляции
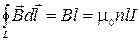
И индукция поля соленоида равна 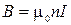 (2.9.4. )
(2.9.4. )
Сила Ампера. Контур с током в магнитном поле.
На каждый движущийся в магнитном поле заряд действует сила Лоренца (2.8.1). Следовательно, на поток таких зарядов также действует сила. Если по аналогии с выводом формулы закона Био – Савара, рассмотреть элемент тока, то на него будет действовать сила
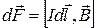 . ( 2.9.5 )
. ( 2.9.5 )
Эта сила называется силой Ампера. Для нахождения силы, действующей на проводник конечной длины нужно просуммировать силы, действующие на все его элементы 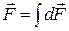 .
.
Рассмотрим, как будет вести себя помещенный в магнитное поле контур с током. Для простоты рассмотрим плоский контур, находящийся в однородном магнитном поле, вектор  лежит в плоскости контура (рис. 2.9.3), т.е. нормаль к контуру
лежит в плоскости контура (рис. 2.9.3), т.е. нормаль к контуру 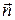 перпендикулярна
перпендикулярна  . Направление нормали связано с направлением тока в контуре правилом правого винта. Разобьем площадь контура на узкие (шириной dy ) полоски, параллельные
. Направление нормали связано с направлением тока в контуре правилом правого винта. Разобьем площадь контура на узкие (шириной dy ) полоски, параллельные  . Выберем одну полоску. На ограничивающий эту полоску элемент тока I
. Выберем одну полоску. На ограничивающий эту полоску элемент тока I 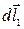 действует сила
действует сила 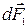 , направленная за чертеж. Ее модуль равен
, направленная за чертеж. Ее модуль равен

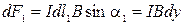 .
.
На элемент 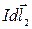 - сила
- сила 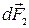 , направленная на нас, ее модуль
, направленная на нас, ее модуль
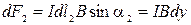 .
.
|
 ∙х=IBdS.
∙х=IBdS.
(dS – площадь полоски).
Вектор 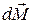 перпендикулярен векторам
перпендикулярен векторам 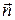 и
и  . Поэтому можно записать
. Поэтому можно записать
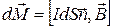 .
.
Просуммировав его по всем полоскам, получим момент сил, действующий на весь контур 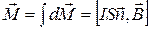 . ( 2.9.6 )
. ( 2.9.6 )
Для характеристики контура с током и его положения в пространстве удобно ввести магнитный дипольный момент 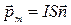 . ( 2.9.7 )
. ( 2.9.7 )
Сам контур в таком случае назовем магнитным диполем.
Тогда формулу (2.9.6) можно переписать
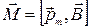 . ( 2.9.8 )
. ( 2.9.8 )
Полученное выражение можно использовать для определения вектора индукции магнитного поля. Из (2.9.8) следует, что, если векторы 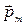 и
и  совпадают по направлению, то вращающий момент, действующий на контур равен нулю, т.е. это положение является положением равновесия контура в магнитном поле. Поэтому, если малый контур с током поместить в магнитное поле и дать ему возможность свободно ориентироваться в поле, то придя в положение равновесия, контур направлением своей положительной нормали укажет направление вектора
совпадают по направлению, то вращающий момент, действующий на контур равен нулю, т.е. это положение является положением равновесия контура в магнитном поле. Поэтому, если малый контур с током поместить в магнитное поле и дать ему возможность свободно ориентироваться в поле, то придя в положение равновесия, контур направлением своей положительной нормали укажет направление вектора  . С помощью той же формулы можно определить и модуль индукции поля. Очевидно, что максимальное значение модуля вращающего момента достигается, если плоскость контура параллельна вектору
. С помощью той же формулы можно определить и модуль индукции поля. Очевидно, что максимальное значение модуля вращающего момента достигается, если плоскость контура параллельна вектору  (
( 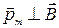 )
) 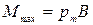 .
.
Тогда, расположив контур указанным образом и определив величину вращающего момента, действующего на него, найдем величину индукции магнитного поля 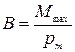 . ( 2.9.9 )
. ( 2.9.9 )
Магнитный диполь (контур с током), находясь в магнитном поле, обладает некоторой энергией. Если сместить контур из положения равновесия, а затем отпустить, то, поворачиваясь обратно, контур может возвратить затраченную на его поворот работу, совершив ее над каким – либо телом. Следовательно, поворачивая контур, мы увеличиваем его потенциальную энергию в магнитном поле. Расчеты показывают, что эту энергию можно определять (по аналогии с электрическим диполем в электрическом поле) по формуле
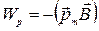 . ( 2.9.10 )
. ( 2.9.10 )
Дата добавления: 2015-08-08; просмотров: 2653;
