Проводник в электростатическом поле. Электроемкость. Конденсаторы.

Истинное электрическое поле в любом веществе (микрополе) меняется весьма заметно во времени и в пространстве. Оно различно в разных точках атомов и промежутках между ними. Напряженность микрополя в данной точке в данный момент времени является суперпозицией напряженностей полей всех отдельно взятых заряженных частиц вещества — электронов и ядер. Решение этой задачи, очевидно, является нереальным. Однако макроскопическая задача решается иначе. Под электрическим полем в веществе (макрополе) будем понимать микрополе, усредненное по физически бесконечно малому объему (объему, содержащему большое число атомов, но имеющему размеры во много раз меньше, чем расстояния, на которых макрополе меняется заметно).

При внесении любого вещества в электрическое поле происходит смещение заряженных частиц вещества. Это явление называют электростатической индукцией. В результате в веществе появляются области зарядов разного знака. Такие заряды называются индуцированными. Индуцированные заряды создают дополнительное электрическое поле, которое вместе с внешним электрическим полем образует результирующее поле.

Свободные и связанные заряды. Проводники и диэлектрики.

В электростатических задачах любое вещество представляет собой пространство, заполненное заряженными микрочастицами. Такие заряды принято делить на свободные и связанные. Во многих веществах существуют свободные заряженные частицы. Свободная частица отличается от связанной тем, что она может передвигаться на большое расстояние под действием сколь угодно малой силы, т.е. сколь угодно слабого электрического поля. Вещества, содержащие свободные заряженные микрочастицы (носители электрического тока), называются проводниками. Проводниками являются металлы, электролиты, плазма. В металлах носителями являются электроны, в электролитических жидкостях – ионы, в плазме – обоих типов. Вещества, где свободные заряды отсутствуют, называются диэлектриками. Необходимо заметить, что такое четкое разделение является идеализацией. Ни идеальных проводников, ни идеальных диэлектриков в природе не существует.

Электростатическое поле внутри проводника.

Поместим проводник во внешнее электростатическое поле 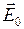или сообщим ему какой-нибудь заряд (см. рис.2.20). В обоих случаях на все заряды проводника будет действовать электрическое поле c силой (2.1.3), и вследствие электростатической индукции отрицательные заряды сместятся против поля, а положительные – по полю. Эти заряды создадут собственное поле с напряженностью 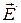(рис. 2.4.1). Тогда результирующее поле в проводнике .

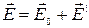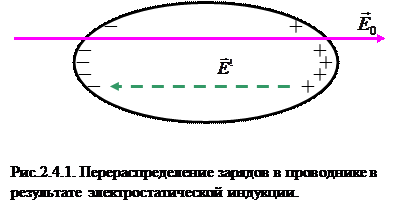
Поэтому смещение зарядов продолжается в течение малой доли секунды и прекращается, как только результирующее поле в проводнике становится равным нулю. (В идеальном проводнике количество свободных зарядов велико настолько, что их всегда достаточно, чтобы скомпенсировать внешнее поле). Так как поле внутри вещества всюду равно нулю, то поток через любую замкнутую поверхность, находящуюся внутри проводника, также будет равен нулю и согласно теореме Гаусса избыточного заряда внутри проводника нет ( ). Избыточные (индуцированные) заряды появляются на поверхности проводника в очень тонком поверхностном слое порядка двух межатомных расстояний.

Отсутствие поля внутри проводника означает согласно (2.1.11), что потенциал 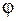в проводнике одинаков во всех его точках. Иными словами любой проводник в электростатическом поле представляет собой эквипотенциальную область, и его поверхность является эквипотенциальной.

Электростатическое поле вне проводника.

Так как поверхность проводника эквипотенциальна, то линии напряженности электростатического поля снаружи направлены по нормали к поверхности проводника в каждой точке. На рис.2.21 показано как изменится структура электрического поля при внесении в него проводника.

Из рис.2.4.2 видно, что проводник искажает внешнее электрическое поле. Силовые линии внешнего поля прерываются. Они заканчиваются на отрицательном индуцированном заряде, а начинаются на положительном.

Напряженность электрического поля непосредственно у поверхности проводника связана с локальной плотностью заряда на его поверхности. Эту связь установим с помощью теоремы Гаусса.

Пусть участок поверхности проводника граничит с вакуумом. Силовые линии перпендикулярны поверхности проводника, поэтому в качестве замкнутой поверхности интегрирования выберем цилиндр, расположив его так, как показано на рис.2.4.3. Площадь

основания цилиндра настолько мала, чтобы можно было пренебречь кривизной поверхности проводника в данной точке, а, сами основания расположены в непосредственной близости от поверхности проводника (одно снаружи, другое внутри), так что высота цилиндра также мала. Поток вектора 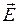через нижнее основание цилиндра равен нулю, так как поля внутри проводника нет. Поток вектора 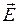через боковую поверхность цилиндра равен нулю, так как силовые линии ее не пересекают. Отличным от нуля будет только поток вектора 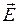через наружное основание цилиндра. Тогда согласно теореме Гаусса можем записать

,

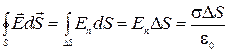где 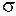- поверхностная плотность заряда на проводнике в данной точке, 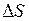-площадь сечения цилиндра, Е 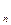- проекция на внешнюю нормаль к поверхности проводника. Из этого соотношения следует

.

( 2.4.1 )

Если , то и 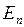>0, т. е. вектор 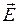направлен от поверхности проводника (совпадает по направлению с нормалью 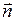); если же 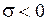, то и 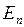<0 ¾ вектор 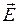направлен к поверхности проводника. (Заметим, что фактически напряженность поля вблизи поверхности проводника как и локальная плотность заряда в данной точке определяется всеми зарядами системы).

Так как напряженность поля внутри проводника равна нулю, то из (2.4.1) можно сделать вывод, что при переходе через заряженную поверхность возникает скачок нормальной составляющей напряженности поля

, ( 2.4.2 )

где нормаль направлена из области 1 в область 2, а - плотность заряда вблизи точки, где осуществляется переход. Необходимо заметить, что это соотношение справедливо не только для заряженной поверхности проводника, но и в случае, когда напряженность поля по обе стороны от некоторой заряженной поверхности отлична от нуля

Свойства замкнутой проводящей оболочки.

Так как в равновесии внутри проводника нескомпенсированных зарядов нет, т. е. вещество электрически нейтрально, то, удалив часть вещества из некоторого объема внутри проводника, мы получим полость, в которой напряженность электрического поля будет равна нулю. Внешние заряды на наружной поверхности проводника не создают поле внутри вещества, в том числе и в полости. На этом основана электростатическая защита. Она заключается в экранировании тел, например измерительных приборов, от влияния внешних электрических полей. Практически сплошной проводник – оболочка может быть заменен достаточно густой металлической сеткой (электростатическая защита Фарадея).

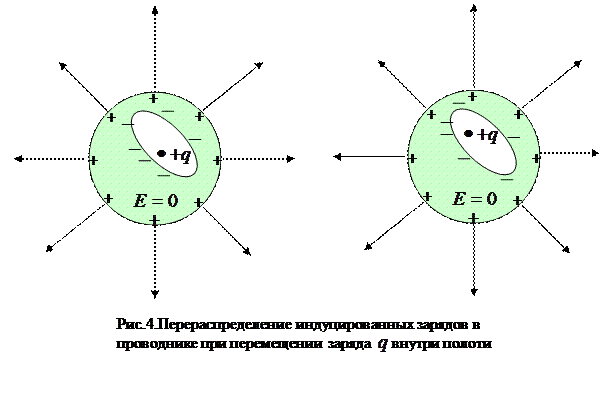Рассмотрим случай, когда в полости есть электрический заряд 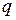. Теперь электрическое поле в полости отлично от нуля. В равновесии электрическое поле в проводнике равно нулю, следовательно, если окружить замкнутой поверхностью полость с зарядом так, чтобы все точки поверхности находились внутри проводящей среды, то поток вектора напряженности электрического поля через такую поверхность будет равен нулю. Согласно теореме Гаусса алгебраическая сумма зарядов, заключенных внутри этой поверхности, также должна быть равна нулю. Таким образом, на поверхности полости появляется индуцированный заряд, равный по модулю и противоположный по знаку алгебраической сумме зарядов внутри этой полости. Следовательно, поле зарядов, заключенных внутри проводящей оболочки и индуцированных на внутренней поверхности оболочки, равно нулю во всем внешнем пространстве. Поскольку суммарный заряд проводника равен нулю, то по наружной поверхности проводника распределен заряд равный заряду, находящемуся в полости и имеющий тот же знак. Если перемещать заряд внутри оболочки, то поле во внешнем пространстве не изменится и, следовательно, не изменится распределение зарядов на внешней поверхности оболочки (см. рис.2.4.4). Таким образом, на внутренней поверхности проводника заряд будет распределен неравномерно, а на внешней равномерно независимо от положения заряда в полости.