Вблизи поверхности заряженного проводника

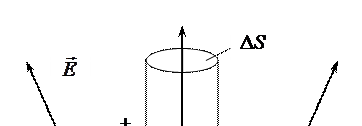Для решения этой задачи целесообразно воспользоваться теоремой Гаусса. Рассмотрим участок поверхности проводника, заряженного положительно (рис. 38.1).

Внутри него электрическое поле отсутствует, а около поверхности линии напряженности перпендикулярны проводнику. Построим цилиндр, основания которого площадью ΔS параллельны поверхности проводника, а боковая поверхность перпендикулярна ей.

Линии напряженности пересекают только основание цилиндра, расположенное вне проводника, и поэтому поток вектора напряженности через замкнутую поверхность цилиндра равен 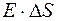. Внутри цилиндра находится участок заряженной поверхности, заряд которого .

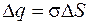По теореме Гаусса, для выбранного цилиндра

.

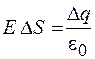Отсюда выразим напряженность поля

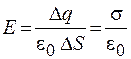. (38.1)

Из формулы (38.1) следует, что напряженность поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности заряда на проводнике. На основании формул (37.1) и (38.1) можно сделать вывод, что напряженность поля около острых выступов может быть настолько большой, что воздух ионизируется. Ионы, заряд которых противоположен заряду проводника, притягиваются к нему и уменьшают его заряд. Ионы с зарядом того же знака, что и на проводнике, напротив, удаляются от проводника и увлекают за собой нейтральные молекулы. В результате возникает движение воздуха, называемое электрическим ветром. Его можно обнаружить по отклонению пламени свечи, поднесенной к острому выступу на проводнике.