Электрический заряд. Его свойства. Закон Кулона. Электростатическое поле, его характеристики.
Исходным пунктом учения об электричестве явилось открытие, что при трении некоторые тела обнаруживают способность притягивать к себе легкие предметы. (Наличие такого свойства у янтаря было известно уже древним грекам, которым мы обязаны терминами «электрон», «электричество», «магнит»). Понимание фундаментальности электромагнитных взаимодействий началось с открытия электрона английским физиком Дж.Дж.Томсоном в конце ХΙХ века и дальнейшего обнаружения элементарных частиц, образующих все тела. В настоящее время известно, что в основе всего разнообразия явлений природы лежат четыре фундаментальных взаимодействия между элементарными частицами – сильное, электромагнитное, слабое и гравитационное. Каждый вид связан с определенным свойством, присущим частице. Электромагнитное взаимодействие обусловлено свойством, названным электрическим зарядом.
Таким образом, электрический заряд частицы является одной из основных, первичных ее характеристик. Опытным путем было установлено, что электрические заряды обладают следующими свойствами:
1. электрический заряд не является знакоопределенной величиной: существуют положительные и отрицательные заряды, причем присутствие в одной системе частиц с зарядами разных знаков может привести к ее электрической нейтральности (заряд системы равен нулю);
2. электрический заряд является релятивистски инвариантным, т.е. при переходе от одной инерциальной системы отсчета к другой величина заряда не меняется;
3. электрический заряд дискретен: все заряды кратны элементарному, величина которого составляет 1,6022∙10 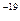 Кл (единицей измерения заряда в системе СИ является Кулон); элементарный заряд был впервые измерен в 1909 г. Р.Милликеном;
Кл (единицей измерения заряда в системе СИ является Кулон); элементарный заряд был впервые измерен в 1909 г. Р.Милликеном;
4. электрический заряд аддитивен: заряд любой системы равен сумме зарядов, ее составляющих;
5. суммарный электрический заряд изолированной системы сохраняется; это утверждение называется законом сохранения электрического заряда.
Все перечисленные свойства являются фундаментальными законами. Они не выводятся из каких-либо других физических законов. Не обнаружено явлений, которые противоречили бы этим свойствам.
Важной идеализацией при изучении законов электродинамики является понятие «точечный заряд». Точечным зарядом называют обладающее электрическим зарядом тело, размерами которого можно пренебречь в условиях данной задачи.
Локальной величиной, характеризующей распределение зарядов, является плотность заряда. Для упрощения математических расчетов бывает удобно игнорировать дискретную структуру зарядов и заменить их истинное распределение фиктивным непрерывным распределением. Тогда можно ввести понятия объемной, поверхностной и линейной плотности заряда. Объемная плотность заряда это заряд, приходящийся на единицу объема системы, определяемый как 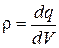 (здесь dq –заряд, заключенный в объеме dV). Если заряд распределен по слою толщиной h и площадью S , причем h мало по сравнению с двумя другими размерами, то dV=h∙dS и
(здесь dq –заряд, заключенный в объеме dV). Если заряд распределен по слою толщиной h и площадью S , причем h мало по сравнению с двумя другими размерами, то dV=h∙dS и 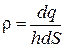 , откуда
, откуда 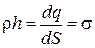 ─ поверхностная плотность заряда, т.е. заряд, приходящийся на единицу поверхности. Аналогично, если в системе один из линейных размеров много больше двух других, то удобно ввести линейную плотность заряда
─ поверхностная плотность заряда, т.е. заряд, приходящийся на единицу поверхности. Аналогично, если в системе один из линейных размеров много больше двух других, то удобно ввести линейную плотность заряда 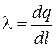 ─ заряд, приходящийся на единицу длины.
─ заряд, приходящийся на единицу длины.
 В общем случае плотность заряда является функцией координат и времени, а для стационарных задач функцией координат (
В общем случае плотность заряда является функцией координат и времени, а для стационарных задач функцией координат ( 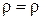 (
( 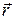 ),
), 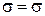 (
( 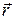 ),
), 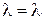 (
( 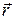 ) ).В отличие от самого заряда плотность заряда не является инвариантной при переходе от одной инерциальной системы отсчета к другой, что является следствием преобразований Лоренца для координат- времени.
) ).В отличие от самого заряда плотность заряда не является инвариантной при переходе от одной инерциальной системы отсчета к другой, что является следствием преобразований Лоренца для координат- времени.
Взаимодействие зарядов. Закон Кулона.
Характер взаимодействия электрических зарядов зависит от характера их движения. Взаимодействие неподвижных зарядов изучает электростатика. Основной закон взаимодействия неподвижных зарядов был экспериментально установлен французским физиком Ш.Кулоном в 1785г. (На 11 лет ранее этот закон был открыт английским ученым Г.Кавендишем, но его труды были опубликованы лишь через 100 лет).
Закон Кулона утверждает:
1. заряды одного знака отталкиваются, а противоположных знаков - притягиваются;
2. сила взаимодействия двух точечных зарядов направлена вдоль прямой, соединяющей эти заряды, прямо пропорциональна величинам этих зарядов 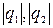 и обратно пропорциональна квадрату расстояния между ними r
и обратно пропорциональна квадрату расстояния между ними r 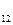 ; величина силы зависит также от свойств среды, в которой находятся заряды.
; величина силы зависит также от свойств среды, в которой находятся заряды.
На рис.2.1.1 показаны силы взаимодействия точечных зарядов. Математически силу, с которой находящийся в вакууме точечный заряд q  действует на точечный заряд q
действует на точечный заряд q 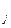 можно записать
можно записать
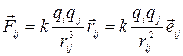 ,
,  ( 2.1.1 )
( 2.1.1 )
где 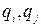 - заряды с учетом знака,
- заряды с учетом знака, 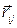 радиус-вектор, проведенный от заряда
радиус-вектор, проведенный от заряда 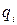 к
к
 заряду
заряду 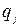 ,
, 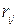 - его модуль,
- его модуль, 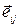 - орт, направленный от заряда
- орт, направленный от заряда 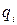 к заряду
к заряду 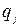 ,
, 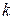 -коэффициент пропорциональности, который зависит от выбора системы единиц (в системе СИ
-коэффициент пропорциональности, который зависит от выбора системы единиц (в системе СИ 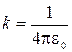 ,где
,где 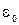 =8,85∙10
=8,85∙10 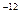
 – физическая константа, называемая электрической постоянной ).
– физическая константа, называемая электрической постоянной ).
Если зарядов не два, а более, то каждый заряд взаимодействует со всеми остальными. Тогда результирующую силу можно найти по принципу суперпозиции, поскольку взаимодействие каждой пары зарядов не зависит от присутствия остальных. На рис.2.1.2 показано, как направлена равнодействующая сил, приложенных к заряду 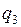 со стороны зарядов
со стороны зарядов 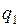 и
и 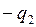 системы.
системы.
Электростатическое поле. Характеристики поля, связь между ними.
Взаимодействие электрических зарядов осуществляется на расстоянии. Для описания явлений такого рода применяется понятие силового поля. Взаимодействие двух частиц трактуется следующим образом. Одна из частиц, находящихся в пространстве, изменяет свойства пространства – создает поле, называемое в рассматриваемом случае электростатическим. Другая частица, попав в это поле , испытывает его воздействие.  __________________________________________________________________
__________________________________________________________________
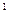 В нерелятивистской механике такой способ описания действия на расстоянии является только удобным формальным приемом. Но с открытием предельной скорости передачи воздействий выяснилось, что поле – это не просто удобный прием описания взаимодействий на расстоянии, а физическая реальность. Поскольку взаимодействие передается с конечной скоростью, то должен существовать материальный объект, переносящий взаимодействие в пространстве с этой скоростью. Осуществляет этот перенос поле, выполняющее роль посредника во взаимодействии пространственно разделенных частиц и представляющее собой особый вид материи. Поскольку электромагнитные взаимодействия осуществляются через электромагнитные поля, то оказывается, что электрический заряд является константой связи заряженных частиц с электромагнитным полем. Поэтому электромагнитные поля возникают вокруг зарядов (как неподвижных, так и движущихся), от которых и распространяются в окружающее пространство, и действуют на заряды.
В нерелятивистской механике такой способ описания действия на расстоянии является только удобным формальным приемом. Но с открытием предельной скорости передачи воздействий выяснилось, что поле – это не просто удобный прием описания взаимодействий на расстоянии, а физическая реальность. Поскольку взаимодействие передается с конечной скоростью, то должен существовать материальный объект, переносящий взаимодействие в пространстве с этой скоростью. Осуществляет этот перенос поле, выполняющее роль посредника во взаимодействии пространственно разделенных частиц и представляющее собой особый вид материи. Поскольку электромагнитные взаимодействия осуществляются через электромагнитные поля, то оказывается, что электрический заряд является константой связи заряженных частиц с электромагнитным полем. Поэтому электромагнитные поля возникают вокруг зарядов (как неподвижных, так и движущихся), от которых и распространяются в окружающее пространство, и действуют на заряды.
Будем вначале рассматривать электростатическое (созданное неподвижными зарядами) поле в вакууме. (Для краткости будем называть его электрическим полем). Опытным путем установлено, что сила, действующая на помещенный в поле заряд, зависит от этого заряда и некоторой характеристики поля. Причем, сила прямо пропорциональна величине заряда, так что отношение силы к величине заряда в данной точке остается неизменным и, следовательно, может служить характеристикой поля. Таким образом вводится силовая характеристика поля как сила, действующая на находящийся в этом поле единичный положительный точечный неподвижный заря. Эта величина называется напряженностью электрического поля. Математически ее можно представить
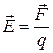 , ( 2.1.2 )
, ( 2.1.2 )
где 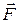 - сила, действующая на находящийся в электростатическом поле заряд q. Из этого определения следует, что силу, действующую на заряд в электрическом поле, можно находить по формуле
- сила, действующая на находящийся в электростатическом поле заряд q. Из этого определения следует, что силу, действующую на заряд в электрическом поле, можно находить по формуле
 . ( 2.1.3 )
. ( 2.1.3 )
Если напряженность поля во всех точках пространства по величине и направлению одинакова, поле называется однородным.
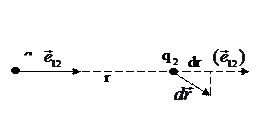 Известно, что любое стационарное поле центральных сил является консервативным, т. е. работа сил этого поля не зависит от пути, а зависит от начального и конечного положения, и может быть представлена через убыль потенциальной энергии. Именно таким свойством обладает электростатическое поле. В качестве примера рассчитаем работу A при перемещении
Известно, что любое стационарное поле центральных сил является консервативным, т. е. работа сил этого поля не зависит от пути, а зависит от начального и конечного положения, и может быть представлена через убыль потенциальной энергии. Именно таким свойством обладает электростатическое поле. В качестве примера рассчитаем работу A при перемещении 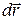 заряда q
заряда q 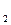 , находящегося в поле, созданном точечным зарядом q
, находящегося в поле, созданном точечным зарядом q 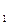 на расстоянии r от него
на расстоянии r от него
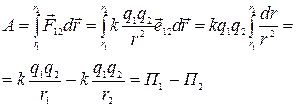
Рис.2.1.3 ( 2.1.3 )
Следовательно, находящийся в поле заряд обладает потенциальной энергией, которая прямо пропорциональна величине этого заряда. Тогда потенциальную энергию единичного положительного точечного неподвижного заряда, находящегося в электростатическом поле, можно считать энергетической характеристикой поля, называемой потенциалом,
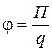 , ( 2.1.4 )
, ( 2.1.4 )
где П - потенциальная энергия точечного заряда q в электростатическом поле. Отсюда следует, что работу поля по перемещению заряда можно представить
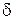 А = - dП = - q
А = - dП = - q 
 ( 2.1.5 )
( 2.1.5 )
Представив работу электрического поля при перемещении заряда через убыль потенциальной энергии, получим с учетом (2.1.2) и (2.1.4) соотношение, связывающее две характеристики электростатического поля
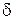 А=
А= 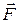
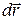 = - dП = q
= - dП = q 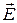
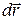 = - q
= - q  ;
;
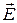
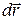 = - d
= - d 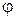 . ( 2.1.6)
. ( 2.1.6)
Отсюда 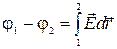 . ( 2.1.7 )
. ( 2.1.7 )
Если же траектория замкнута, то циркуляция 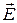 равна нулю
равна нулю
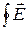
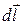 =
= 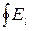 dl = 0, ( 2.1.8 )
dl = 0, ( 2.1.8 )
где 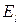 - проекция вектора напряженности на направление обхода по контуру,
- проекция вектора напряженности на направление обхода по контуру, 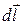 - элементарное перемещение по контуру.
- элементарное перемещение по контуру.
Это соотношение указывает на потенциальность электростатического поля.
В декартовой системе координат соотношение ( 2.1.6 ) можно записать
 E
E 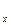 dx + E
dx + E 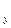 dy + E
dy + E  dz = - d
dz = - d 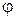 , ( 2.1.9 )
, ( 2.1.9 )
откуда следует 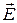 = - (
= - ( 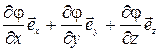 ). ( 2.1.10 )
). ( 2.1.10 )
Кроме того, проекцию вектора напряженности на произвольное направление можно выразить через производную потенциала по этому направлению
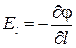 . (2.1.11 )
. (2.1.11 )
Формулы ( 2.1.4 ) и ( 2.1.6 ) можно использовать для установления единиц измерения напряженности и потенциала поля. В системе СИ единицей потенциала является вольт (сокращенное обозначение – В): 1 В = 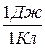 , единицей напряженности ─
, единицей напряженности ─ 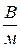 , что следует из ( 2.1.6 ).
, что следует из ( 2.1.6 ).
Графическое представление электрического поля. Силовые линии и эквипотенциальные поверхности.
Существует графический способ представления электрического поля с помощью силовых линий и эквипотенциальных поверхностей.
Силовые линии или линии напряженности проводят так, чтобы касательная к ним в каждой точке совпадала с направлением вектора 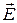 . Густота линий выбирается так, чтобы количество линий, пересекающих единичную поверхность, перпендикулярную к силовым линиям, было пропорционально численному значению напряженности. Воображаемая поверхность, во всех точках которой потенциал имеет одно и то же значение, называется эквипотенциальной или поверхностью равного потенциала.
. Густота линий выбирается так, чтобы количество линий, пересекающих единичную поверхность, перпендикулярную к силовым линиям, было пропорционально численному значению напряженности. Воображаемая поверхность, во всех точках которой потенциал имеет одно и то же значение, называется эквипотенциальной или поверхностью равного потенциала.
Из ( 2.1.11 ) следует, что проекция вектора напряженности на направление касательной к эквипотенциальной поверхности равна нулю, поскольку при перемещении вдоль эквипотенциальной поверхности потенциал не меняется. Отсюда 
 следует, что вектор
следует, что вектор 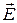 перпендикулярен эквипотенциальной поверхности, а, следовательно, силовые линии в каждой точке ортогональны эквипотенциальным поверхностям. Проекция же вектора
перпендикулярен эквипотенциальной поверхности, а, следовательно, силовые линии в каждой точке ортогональны эквипотенциальным поверхностям. Проекция же вектора 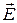 на направление нормали к эквипотенциальной поверхности равна производной потенциала по направлению нормали со знаком минус, т.е. вдоль силовой линии потенциал убывает, причем, быстрее, чем в любом другом направлении.
на направление нормали к эквипотенциальной поверхности равна производной потенциала по направлению нормали со знаком минус, т.е. вдоль силовой линии потенциал убывает, причем, быстрее, чем в любом другом направлении.
Дата добавления: 2015-08-08; просмотров: 2611;
