Теорема о проекциях скоростей двух точек тела
Из доказанной теоремы вытекает следствие: проекции скоростей концов неизменяемого отрезка на направление этого отрезка равны между собой.
Действительно, так как относительная скорость υOM перпендикулярна к радиусу - вектору ОМ = rOM, то, проектируя обе части векторного равенства (11.95) на направление отрезка ОМ, получим
пp υM(ОМ) = пр υ0(ОМ).
План скоростей
В инженерной практике при определении скоростей точек плоских механизмов пользуются графическим методом, именуемым планом скоростей.
План скоростей — это чертеж, изображающий векторы скоростей точек плоской фигуры в фиксированный момент времени ее движения. Для построения плана скоростей нужно знать величину и направление скорости одной точки и направление скорости второй точкой плоской фигуры. Затем следует применить теорему о нахождении скоростей точек тела при плоско – параллельном движении.
Пусть в некоторый момент времени задана скорость точки А и направление скорости точки В плоской фигуры. Требуется найти величину скорости υВ точки В и скорость υС любой точки С (рис.72, а). Выбирая точку А за полюс, по формуле (ІІ.95) получим
υВ=υА+υАВ
где скорость υАВ перпендикулярна АВ.

Из произвольного полюса О в выбранном масштабе откладываем вектор Оа=υА (рис. 72, б). Из точки а проводим прямую ab , перпендикулярную АВ, а из полюса – прямую, параллельную направлению искомой скорости точки В до взаимного пересечения в точке b. Вектор Оb представляет собой в выбранном масштабе скорость точки b: Оb=υВ. Вектор ab равен скорости точки В во вращательном движении вокруг точки А, т.е. ab=υАВ. Так как скорость точки С неизвестна ни по величине, ни по направлению, то составим для ее определения два уравнения, выбирая сначала за полюс точку А, а затем – точку В, и применяя формулу (ІІ.95). Получим υС=υА+υАС, υС=υВ+υВС , где υАС – перпендикулярна АС и υВС – перпендикулярна ВС. Тогда соответственно из точек а и b проводим прямые, перпендикулярные АС и ВС до взаимного пересечения в точке с (рис. 72, б). Вектор Осв выбранном масштабе равен скорости точки С: Ос=υС. Соответственно ас=υАС, bc= υВС. Полученная фигура называется планом скоростей. На плане скоростей получается фигура, подобная данной, но повернутая на угол 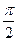 в сторону вращения рассматриваемой плоской фигуры. Действительно, треугольник abc на плане скоростей подобен треугольнику АВС плоской фигуры. Отношение подобие этих фигур равна величине угловой скорости вращения плоской фигуры, т.е.
в сторону вращения рассматриваемой плоской фигуры. Действительно, треугольник abc на плане скоростей подобен треугольнику АВС плоской фигуры. Отношение подобие этих фигур равна величине угловой скорости вращения плоской фигуры, т.е.
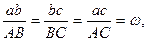
или
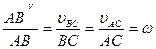
Дата добавления: 2015-08-08; просмотров: 1332;
