Мгновенный центр скоростей и способ его нахождения
Из построения плана скоростей вытекает, что в каждый момент существует точка плоской фигуры, скорость которой равна нулю. Этой точке плоской фигуры соответствует полюс на плане скоростей.

Точкой плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей (МЦС). Условимся обозначать его буквой Р. Положение мгновенного центра скоростей можно определить двумя геометрическими способами: 1) по заданной скорости какой – либо точки плоской фигуры и мгновенной угловой скорости вращения этой фигуры; 2) по известным направлениям скоростей двух точек плоской фигуры.
Первый способ. Пусть заданная скорость υА точки А плоской фигуры и мгновенная угловая скорость ωвращения фигуры вокруг точки А (рис. 73, а). Тогда по формуле (ІІ.95) получим для мгновенного центра скоростей Р
υР= υА+ υАР.
Но, по определению точки Р, υР=0. Следовательно,
υАР= -υА
откуда
υАР= υА
где
υАР= ω·АР
Следовательно,
ω·АР= υА
Откуда расстояние мгновенного центра скоростей Р от точки А равно
АР= 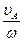
Итак, мгновенный центр скоростей находится на перпендикуляре, проведенном из начала вектора скорости заданной точки А на расстоянии, равном отношению модуля скорости заданной точки к модулю угловой скорости.
Второй способ.Пусть заданы направления скоростей двух точек А и В (рис. 73, б) движущейся плоской фигуры. Требуется определить положение мгновенного центра скоростей. Выбирая в качестве полюса точку Р, по формуле (ІІ.95) получим
υА = υР + υАР , υВ= υР+ υРВ.
Но υР=0, следовательно,
υА= υРА , υА= υРВ
т.е. скорости точек А и В можно рассматривать как скорости в их вращательном движении вокруг мгновенного центра скоростей Р. Так как эти скорости перпендикулярны к отрезкам, соединяющим заданные точки с мгновенным центром скоростей Р, то мгновенный центр скоростей находится в точке пересечения перпендикуляров, проведенных из начала векторов скоростей двух точек плоской фигуры,
Так как
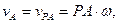

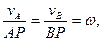
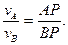
Дата добавления: 2015-08-08; просмотров: 1385;
