Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси

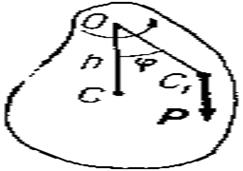
Пусть твердое тело вращается вокруг неподвижной оси под дей­ствием внешних сил F₁, F₂,…,F_n (рис. 114). В этом случае тело имеет одну степень свободы (k =1) и за обобщен­ную координату примем угол поворота (q=φ).

Кинетическая энергия тела будет

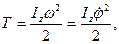
где I_z — момент инерции тела относительно оси вра­щения z.

Обобщенную силу Q найдем из формулы

где М_z — главный момент приложенных к телу внешних сил отно­сительно оси z. Имеем

Q=M_z.

Подставляя в уравнение Лагранжа

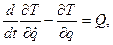
получим дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси

I 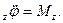2Ф = М2. | Ш.218

Предлагаем читателю самостоятельно вывести дифференциальное уравнение вращательного движения твердого тела вокруг неподвиж­ной оси на основании теоремы об изменении кинетического момента

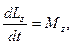где по (111.97) L_z=I_zω