Дифференциальные уравнения вращательного движения твердого тела вокруг неподвижной точки (динамические уравнения Эйлера)

Для вывода дифференциальных уравнений вращательного дви­жения твердого тела вокруг неподвижной точки воспользуемся уравнениями Лагранжа второго рода

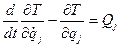(j=1,2,…,λ).

и совместим подвижные координатные оси Oξ, Oη, Oζ неизменно связанные с телом, с его главными осями инерции относительно неподвижной точки О.

Из кинематики известно (ч. II, гл. VI, § 2), что положение твер­дого тела с неподвижной точкой определяется тремя углами Эйлера, которые примем за обобщенные координаты

q₁=ψ, q₂= θ, q₃=φ.

Тело в рассматриваемом случае имеет три степени свободы (k = 3).

В соответствии с формулами (111.118), кинетическая энергия тела равна

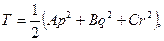
где А =I_ξ , В =I_η, С=I_ζ - главные моменты инерции тела от­носительно подвижных осей, р=ω_ξ, q=ω_η, r=ω_ζ -проекции угловой скорости вращения тела на подвижные оси, определяемые из кинематических уравнений Эйлера

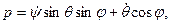
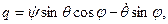
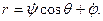
Вычислим частные производные

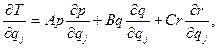
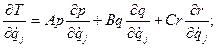
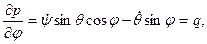
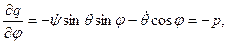
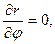
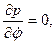
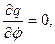
так что

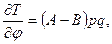
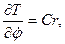
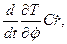
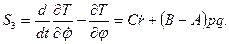
Аналогично получим:

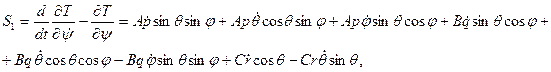
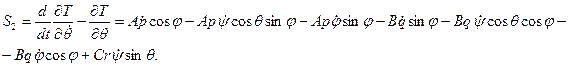
В соответствии с теоремой Эйлера о перемещении тела с неподвиж­ной точкой (ч. II, гл. VI, § 1)

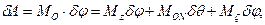
следовательно, обобщенные силы соответственно будут

Q₁=M_z, Q₂=M_ON, Q₃=M_ζ,

где M_z, M_ON, M_ζ— главные моменты приложенных к телу внешних сил относительно неподвижной оси О_z, линии узлов ОN и подвижной оси O_ζ.

Таким образом, уравнения Лагранжа второго рода в рассматри­ваемом случае будут

S₁=M_z, S₂=M_N, S₃=M_ζ.

Из трех полученных дифференциальных уравнений первые два очень громоздкие, в то время как третье уравнение

имеет чрезвычайно простую, симметричную форму и оно явно не со­держит компоненты угловой скорости тела p,q,r. Очевидно, слож­ность записи первых двух уравнений объясняется тем, что в правых частях этих уравнений вместо моментов М_ξ, М_η фигурируют

отличные от них обобщенные силы М_z и М_N. Однако путем надлежа­щего преобразования г эти уравнения можно привести к форме, аналогичной третьему уравнению.

Итак, дифференциальные уравнения вращательного движения твердого тела вокруг неподвижной точки принимают вид

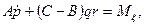
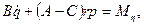
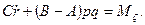
Эти уравнения называются динамическими уравнениями Эйлера. Заметим, что уравнения Эйлера можно также вывести, применив теорему об изменении кинетического момента.