О допущениях в приближенной теории гироскопов

Рассмотрим вращение гироскопа вокруг неподвижной точ­ки О, лежащей на оси симметрии O_ξ, (рис. 123), с угловой скоростью ω₁.В свою очередь ось симметрии O_ζ вращается вокруг вертикальной оси Оz с угловой скоростью ω₂, весьма малой по сравнению с ω₁. Следует заметить, что гироскопы, применяемые в современной технике, имеют большую скорость вращения вокруг оси материальной симметрии по сравнению с угловыми скоростями относительно других осей.

Для применения гироскопа нужно знать движение его оси. Это движение можно изучить, зная кинетический момент ги­роскопа относительно его неподвижной точки. Однако угло­вые скорости прецессии ω₂=ψ и нутации ω₃=θ очень малы по сравнению с угловой скоростью ω₁=φ собственного вращения (ω₁»ω₂; ω₁»ω₃). Угол нутации θ также медленно изменяется и приближенно его можно считать постоянным.

По формуле (11.112) мгновенная угловая скорость ω гироскопа равна

ω= ω₁+ω₂+ω₃.

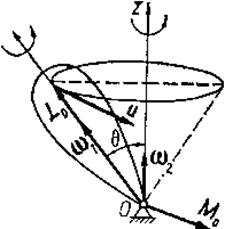
Из-за малости ω₂ и при θ = соnst, ω₃ = θ приближенно можно принять, что ω≈ω₁. Поэтому в приближенной теории гироскопа результирующую мгновенную угловую скорость о направляют по оси симметрии гироскопа

Указанному допущению кинематического характера соответствует следующее допущение динамического характера: проекция кинетического момента гироскопа L₀ относительно неподвижной точки О на ось симметрии гироскопа O_ζ, значительно превышает его проекции на оси O_ξ и О_η:

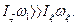
Это условие является основным в приближенной тео­рии гироскопов. Оно равносильно тому, что кинетичес­кий момент гироскопа относительно неподвижной точки мало отклоняется от оси симметрии O_ζ. Поэтому кинетический момент L₀ направляют по оси O_ζ и выражают формулой

L_O=I_ζω₁.

В приближенной теории гироскопа прецессию оси гироскопа счи­тают регулярной, т. е. ось O_ζ, (рис. 124) равномерно вращается во­круг вертикальной оси Оz с угловой скоростью ω₂, описывая поверх­ность кругового конуса. Кроме того, пренебрегают нутацией, полагая θ =α =соnst. Следует заметить, что движение гироско­па является одним из примеров регулярной прецессии.