Гипотеза Ньютона о коэффициенте восстановления
Пусть о неподвижную плоскость ударяется тело, которое будем считать материальной точкой. Обозначим скорость падения υ, скорость отражения u, угол падения α, а угол отражения β (рис. 134).
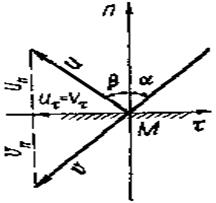
Мгновенной силой при рассматриваемом ударе является реакция поверхности. Так как мгновенным трением можно пренебречь, то мгновенной силой является нормальная реакция N.
Применяя к движущейся точке теорему об изменении количества движения за время удара τ, получим
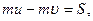
где 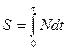 - импульс мгновенной силы N , направленной по нормали n к плоскости.
- импульс мгновенной силы N , направленной по нормали n к плоскости.
Векторы u, υи nлежат в одной плоскости. Поэтому, проектируя обе части этого равенства на направления нормали n и касательной τ, получим два уравнения:
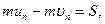
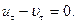
Из второго уравнения видим, что

т. е. касательные составляющие скоростей точки до и после удара равны между собой. Для определения же нормальных составляющих un и υn имеем лишь одно первое уравнение. Чтобы найти un и υn, необходимо к этому уравнению добавить еще одно уравнение, в котором были бы учтены физические (в первую очередь упругие) свойства материала падающего тела и плоскости, о которую оно ударяется. Это недостающее уравнение дал И. Ньютон в виде
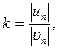
где величина k, равная отношению абсолютных величин нормальных составляющих скорости точки М после удара un и до удара υn, называется коэффициентом восстановления при ударе и определяется опытным путем.
Как показывают опыты, коэффициент восстановления не может быть больше единицы и, в зависимости от материала соударяющихся тел, принимает значения от 0 до 1:
0≤k≤1,
причем
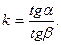
Дата добавления: 2015-08-08; просмотров: 1510;
