Прямой удар двух шаров

Удар двух шаров называется прямым, если скорости их центров инерции направлены по прямой, соединяющей эти центры. Как пока­зал Н. Е. Жуковский, все положения об ударе шаров могут быть пере­несены на удар каких-либо тел.

Пусть скорость центра инерции первого шара до удара—υ₁, а пос­ле удара—u₁ , масса первого шара — m₁, второго шара — m₂, скорость до удара — υ₂, а после удара — u₂. В соответствии с определением прямого удара скорости центров инерции этих шаров направлены по прямой, соединяющей эти центры. Мгновенными силами при ударе этих тел являются силы давления одного шара на другой, им­пульсы которых обозначим через S.

Для определения скоростей соударяющихся тел после удара u₁, u₂, а также импульсов мгновенных сил S рассмотрим движение каж­дого тела в отдельности. Применяя теорему импульсов в проекции на ось С₁х, получим

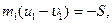
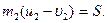
Складывая эти уравнения, найдем основное уравнение Ньютона (в теории удара)

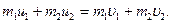
Из (111.261) видим, что количество движения материальной си­стемы при ударе не изменяется.

Это утверждение следует также из того, что при ударе двух тел действуют мгновенные силы, являющиеся внутренними силами в данной системе, а внутренние силы не могут изменить количество дви­жения системы. Однако одного уравнения (111.298) недостаточно для изучения прямого удара двух тел, так как из этого уравнения нельзя определить u₁ и u₂ т. е. скорости тел после удара.

Второе уравнение вводится на основании гипотезы Ньютона о ко­эффициенте восстановления k, который равен

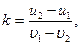
где u₂ — u₁ и υ₁ — υ₂ — соответственно проекции относительных ско­ростей на ось С₁х соударяющихся тел до и после удара.