Вторая задача К. Э. Циолковского

Допустим, что тoчка переменной массы движется по вертикали вверх в однородном поле силы тяжести. Требуется определить закон движения этой точки, г. е. закон изменения скорости и расстояния (высоты) точки переменной массы в функции времени при различных законах изменения ее массы.

Относительная скорость υ_r отбрасываемых частиц принимается постоянной по величине и направленной по вертикали вниз.

Примем прямую, по которой движется точка перемен­ной массы, за ось OS (рис. 139).

Проектируя уравнение (111.311) на ось 08 и принимая во внимание, что F=m (t)g, получим

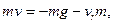
или

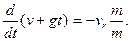
Интегрируя это уравнение при начальных условиях t = О,

υ = О и m (0) = m₀, получим

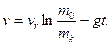
В конце периода отбрасывания, т. е. при t =t_k масса точки переменной массы будет m = m_k, а скорость ее

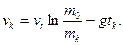
Из сопоставления формул (111.313) и (111.314) видим, что часть отбрасываемой массы в (111.314) должна быть израсходована на «по­крытие» скорости gt_k, вызванной однородным полем силы тяготения, следовательно, для сообщения заданной величины скорости υ_k точ­ки переменной массы необходимо отбросить из нее большее количе­ство массы m_r (m₀ = m_k +m_r).

Для того, чтобы точка переменной массы начала двигаться вер­тикально вверх, очевидно, необходимо, чтобы

Φ - F≥0,

т. е.

mg + υ_rm = 0.

Знак равенства соответствует предельному положению равновесия точки переменной массы. Интегрируя это уравнение в случае равно­весия при условии, что m (0) = m₀, получим

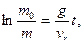
или

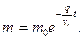
Следовательно, если процесс отбрасывания частиц точки перемен­ной массы будет происходить по закону (111.315), то эта точка будет находиться в покое. Для того чтобы она смогла двигаться вверх, необходимо, чтобы процесс отбрасывания частиц был более интен­сивным, чем это дается законом (111.315).

Рассмотрим процесс отбрасывания частиц по закону

где n — положительное число больше единицы. При m (t) в (111.316) величина реактивной силы Ф будет

Ф = — υ_rm =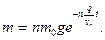

Ускорение точки переменной массы, вызванное реактивной силой Ф,

будет

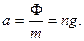
Отсюда видим, что величина

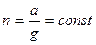
характеризует так называемую перегрузку, вызванную реактивной силой Ф.

Чтобы найти закон изменения расстояния, т. е. функцию s (t), необходимо задать закон изменения массы m (t).

Допустим, что масса точки изменяется по закону, который вы­ражается уравнением (111.316). Таким образом, из (111.316), получим

υ= s = (n — 1) gt.

Интегрируя это уравнение и учитывая начальные условия (при t = О s = 0), получим

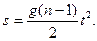
Из формулы Циолковского в виде (111.313) или в более общем виде (111.314), которую удобно представить как

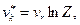
где 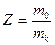— число Циолковского, а 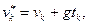следуют два важных практических вывода о том, что увеличение относительной скорости отбрасывания частиц υ_r и уменьшение времени их отбра­сывания t_k оказывает большее влияние на величину конечной ско­рости υ_k движения точки переменной массы, чем увеличение числа Циолковского Z. В этом можно убедиться путем простых подсчетов. В самом деле, например, из (111.313) видим, что увеличение относитель­ной скорости отбрасывания υ_r частиц, например, вдвое, увеличивает скорость υ_k = υ_max также вдвое, т. е. 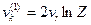, а увеличение числа Циолковского вдвое увеличивает уа лишь согласно формуле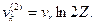

Поэтому в настоящее время наряду с улучшением конструкции ракет, применением новых легких высокопрочных материалов, что ведет к относительному уменьшению массы m_k, наибольшее внимание уделяется исследованию физических явлений, которые могли бы стать источниками энергии для реактивных двигателей и дали бы возможность осуществить на практике теоретически максимально возможную скорость отбрасывания частиц υ_r, равную υ_r = с, где с = 3 • 10⁸ м/с — скорость распространения света (в пустоте).