Первая задача К. Э. Циолковского

Рассмотрим движение точки переменной массы в безвоздушном пространстве, на которую не действуют никакие внешние силы, счи­тая при этом, что относительная скорость υ_r отделения частиц посто­янная по величине, коллинеарна вектору скорости υ излучающей точки и направлена в сторону, противоположную этому вектору.

Приняв в уравнении (111.311) F = 0, получим

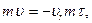
где υ_r = ‌‌‌‌‌‌‌‌Iυ_rI‌ = соnst, τ — единичный вектор касательной к траек­тории движения излучающей точки.

В проекции на касательную к траектории это уравнение после некоторых упрощений примет вид

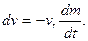
Интегрируя уравнение при начальных условиях t = О, υ = О и m (0) = m₀, найдем

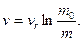
Из (111.312) следует, что наибольшее значение скорость υ точки бу­дет иметь в конце процесса отбрасывания частиц. Если обозначить через m_k массу точки переменной массы в конце процесса отбрасы­вания, ТО ДЛЯ υ_max

ПОЛУЧИМ

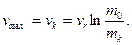
Эта формула впервые была получена К, Э. Циолковским и опубли­кована в 1903 г.