Вторая краевая задача (задача Неймана)

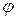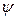На контуре Г, ограничивающем область течения, задана непрерывная функция P(x,y). Требуется найти функцию (или ), удовлетворяющую внутри области течения уравнению Лапласа, нормальная производная которой или 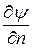на границе принимает заданные значения P(x,y).

Таким образом, непосредственное определение поля скоростей заключается в решении уравнения Лапласа (9.10) или (Д.2.7) для определения φ(x,y) или ψ(x,y), удовлетворяющих граничным условиям данной задачи. Однако в большинстве практических случаев это является невыполнимой задачей. В связи с этим применяется косвенный способ решения задач. Выбирается произвольный потенциал скорости φ(x,y), который удовлетворяет уравнению Лапласа, и строится картина линий тока. Если находятся линии тока, которые совпадают с твёрдыми поверхностями канала или обтекаемого тела, то выбранная функция удовлетворяет граничным условиям задачи и является её решением. В этом случае поле скоростей определяется по формулам

, , .

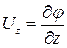Если же не будут найдены линии тока, совпадающие с твёрдыми поверхностями, то выбранная φ(x,y) не является решением задачи; угадывание решений достаточно сложных задач невозможно.