Малые колебания физического и математического маятников

Физическим маятником называется твердое тело любой формы, имеющее горизонтальную ось вращения, не проходящую через центр тяжести тела, называемую осью привеса.

Рассмотрим движение физического маятника под действием силы тяжести Р (рис. 115). В соответствии с (111.218) дифференциальное уравнение движения физического маятника будет

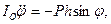
где I_O — момент инерции маятника относительно оси вращения О,

h — расстояние центра инерции С от оси вращения (длина физиче­ского маятника).

При малых колебаниях маятника или при малых углах отклоне­ния φ можно принять sin φ ≈ φ, тогда

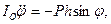
или

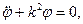
где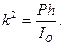

Интегрируя это уравнение, найдем

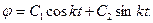
Постоянные интегрирования С₁ и С₂ определим из начальных условий движения. Например, пусть при t = 0, φ₀=α, φ₀₌0.

Тогда

φ=α coskt

Следовательно, под действием силы тяжести (без учета силы сопротивления среды) маятник совершает гармонические колеба­ния. Частота этих колебаний

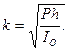
Период Т малых колебаний физичесйого маятника равен

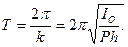
Формула (111.222) может быть использована для опытного опре­деления момента инерции твердого тела.

Математический маятник представляет собой несвободную тяже­лую материальную точку М, соединенную с горизонтальной осью вращения (осью привеса) z гибкой нерастяжимой невесомой нит (или абсолютно жестким невесомым стержнем), движущуюся в вер­тикальной плоскости. Расстояние материальной точки от оси вра­щения называется длиной математического маятника.

Пусть вес математического маятника равен Р, а длина — l. Рассматривая математический маятник как частный случай физи­ческого маятника, применим для вывода дифференциального урав­нения движения математического маятника уравнение (111.219), в котором

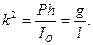
Тогда получим

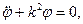или

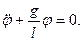
Таким образом, движение математического маятника описывается дифференциальным уравнением, аналогичным уравнению движения физического маятника.

Для круговой частоты колебаний /с и периода колебаний Т ма­тематического маятника получим

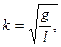
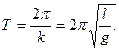
Приведенной длиной физического маятника называется длина синхронного с ним математического маятника, т. е. математического маятника, имеющего тот же период колебаний, что и физический маятник.

Приравняв периоды колебаний математического и физического маятников или выражения (111.224) и (111.222), получим

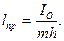
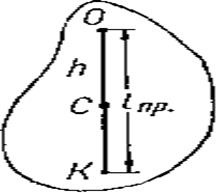
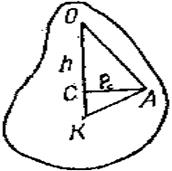
На расстоянии приведенной длины /пр от точки привеса О (рис. 116) находится точка К, которая называется центром коле­баний (качаний) физического маятника.

Центр колебаний физического маятника имеет следующие свой­ства:

1. Центр тяжести маятника расположен между центром колеба­ний и точкой привеса, следовательно l_пр>h.

2. Если заставить маятник колебаться вокруг оси, проходящей через центр колебаний и параллельной его оси привеса, то точка привеса О будет новым центром колебаний такого физического маят­ника.

Это свойство взаимозаменяемости точки привеса и центра коле­баний физического маятника (теорема Гюйгенса) используется в оборотном маятнике Картера, применяемом для определения ускоре­ния силы тяжести в различных точках земной поверхности.

Рассмотрим графический способ нахождения центра колебаний физического маятника, основанный на том, что радиус инерции маятника относительно центральной оси ρ_c есть средняя пропорцио­нальная между длиной h маятника и расстоянием КС его центра инерции от центра колебаний (рис. 116).

Действительно, согласно

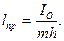
а на основании формулы (111.80)

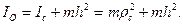
Следовательно,

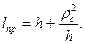
Поэтому

Как видно из рис. 116, l_пр-h=KC=h₁. Поэтому 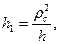откуда

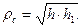
Для нахождения центра колебаний отложим из точки С перпен­дикулярно к отрезку h отрезок рс (рис. 117) и конец его А соединим с точкой привеса О. Затем под прямым углом к ОА проведем прямую до пересечения с продолжением ОС в искомой точке К — центре колебаний физического маятника. Заметим при этом, что ρ_c можно отложить как вправо, так и влево от точки С.