Теорема. Если a сравнимо с b по модулю m, то разность a – b делится на m и наоборот, если разность a – b делится на m
Если a сравнимо с b по модулю m, то разность a – b делится на m и наоборот, если разность a – b делится на m, то а сравнимо с b по модулю m.
Доказательство.
1) Пусть 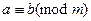 . Это означает, что
. Это означает, что 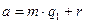 ,
, 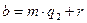 , 0≤r<m.
, 0≤r<m.
Тогда 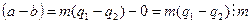 .
.
2) Пусть 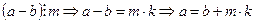
Представим число b в виде
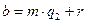 . (а)
. (а)
Тогда
 . (б)
. (б)
Представления (а) и (б), означают, что 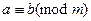 .
.
Дата добавления: 2015-08-01; просмотров: 808;
