Следствие2.

К одной части сравнения можно прибавлять или вычитать из нее любое число, кратное модулю.

3. Сравнения с общим модулем можно почленно перемножать. То есть если 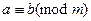, , 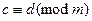то .

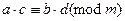Это свойство справедливо и для n сравнений.

4. Обе части сравнения можно делить на их общий делитель, если он взаимно прост с модулем m. То есть, если 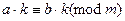и (k,m)=1, то .

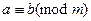5. Обе части сравнения и модуль можно умножить на одно и тоже целое положительное число. То есть, если 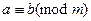, то .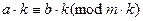

6. Обе части сравнения и модуль можно делить на любой их общий делитель. То есть, если 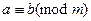, , 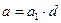, , 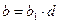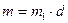то .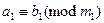

7. Если числа сравнимы по нескольким модулям, то они сравнимы по модулю, равному НОК (наименьшее общее кратное) данных модулей. То есть, если

,

,

………………

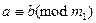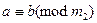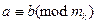, то

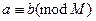, где

.

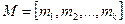8. Если одна часть сравнения и модуль делятся на какое-либо число, то и другая часть сравнения делится на это число.