Доказательство. Выпишем произведение чисел кратных p,
1) n!=1∙2∙3…p…2∙p…3∙p…kp…n.
Выпишем произведение чисел кратных p,
p∙2p∙3p∙…∙kp = 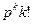 .
.
а все остальные числа не содержат p.
kp≤n, k≤ 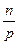 ,
,
k – наибольшее целое не превосходящее 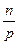 . Значит
. Значит 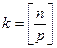 .
.
2) Повторим рассуждения с k! Тогда выделится 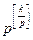 , но
, но
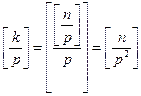
и так далее продолжим наши рассуждения до 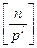 .
.
Далее будут 0, так как
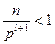 .
.
Итак,
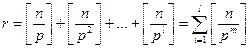 .
.
Дата добавления: 2015-08-01; просмотров: 560;
