Решето Эратосфена.
Для составления таблицы простых чисел, не превосходящих данного целого N, существует простой способ, называемый решетом Эратосфена. Он состоит в следующем:
1. Выписываем числа
1,2,…,N. (1)
Первое большее 1 число этого ряда есть 2. Оно делится только на 1 и на самого себя, следовательно, оно простое. Вычеркиваем из ряда (1), (как составные) все числа кратные 2, кроме самого числа 2. Первое следующее за двойкой не вычеркнутое число есть 3. Оно не делится на 2, (иначе оказалось бы вычеркнутым). Следовательно, три делится только на 1 и на самого себя, а поэтому оно так же будет простым. Вычеркиваем из (1) все числа кратные 3, кроме самой тройки. Первое следующее за 3 не вычеркнутое число есть 5, оно не делится ни на 2, ни на 3 (иначе было бы вычеркнутым). Следовательно, 5 делится на 1 и на самого себя, а потому оно также будет простым и так далее.
Когда указанным способом уже вычеркнуты все числа кратные простых чисел меньших простого p, то все не вычеркнутые меньшие 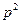 , будут простыми. Действительно, всякое составное
, будут простыми. Действительно, всякое составное 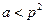 нами уже вычеркнуто, как кратное его наименьшего простого делителя, который
нами уже вычеркнуто, как кратное его наименьшего простого делителя, который 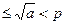 .
.
Отсюда следует:
1. Приступая к вычеркиванию кратных простого p, это вычеркивание следует начинать 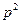 .
.
2. Составление таблицы простых чисел не превосходящих N закончено как только вычеркнуты все составные кратные простых, не превосходящих 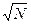 .
.
Дата добавления: 2015-08-01; просмотров: 735;
