Алгоритм Евклида
Алгоритм Евклида применяется для нахождения НОД, а так же для вывода его важнейших свойств. Он состоит в следующем. Пусть a и b – натуральные числа, причем a > b. Запишем ряд равенств
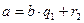
 ,
, 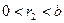 ,
,
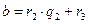
 ,
,  ,
,
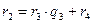
 ,
, 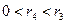 ,
,
………………………………..…… (1)
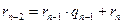
 ,
, 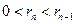 ,
,
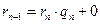
 ,
,
заканчивающийся, когда получится некоторое 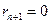 . Последнее неизбежно, так как числа
. Последнее неизбежно, так как числа 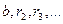 целые положительные и убывают, значит этих чисел не более чем b штук. Рассматривая равенства (1), идя сверху вниз, убеждаемся что общие делители a и b одинаковы с общими делителями чисел b и
целые положительные и убывают, значит этих чисел не более чем b штук. Рассматривая равенства (1), идя сверху вниз, убеждаемся что общие делители a и b одинаковы с общими делителями чисел b и 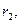 далее одинаковы с общими делителями чисел
далее одинаковы с общими делителями чисел 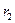 и
и 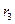 , чисел
, чисел 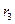 и
и 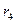 ,…, чисел
,…, чисел 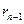 и
и 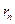 , наконец с делителями одного числа
, наконец с делителями одного числа 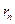 , являющегося последним не равным нулю остатком алгоритма Евклида. Одновременно с этим имеем (a,b) = (b,
, являющегося последним не равным нулю остатком алгоритма Евклида. Одновременно с этим имеем (a,b) = (b, 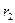 ) = (
) = ( 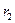 ,
, 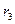 ) =…= (
) =…= ( 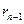 ,
, 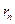 ) =
) = 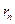 . Мы приходим к следующим результатам
. Мы приходим к следующим результатам
1. Совокупность общих делителей чисел a и b совпадает с совокупностью делителей их общего наибольшего делителя.
2. Этот наибольший общий делитель равен последнему, не равному 0 остатку алгоритма Евклида.
Дата добавления: 2015-08-01; просмотров: 585;
