Доказательство. Обозначение: d|a – d делит a, – a делится на d.
Лекция №15-16
Теория делимости.
Определение.
Пусть a и d – целые числа. Говорят, что d – делитель a, или что d делит a, или что a кратно d, или что a делится на d, если существует такое число c, что a = d ∙ c.
Обозначение: d|a – d делит a, 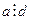 – a делится на d.
– a делится на d.
Пример 1.
Докажите, что если d|a, d|b, то d|(a+b) и d|(a-b).
Доказательство.
Так как d|a, то существует целое число 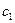 такое что
такое что 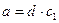 . Так как d|b, то существует целое число
. Так как d|b, то существует целое число 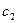 , такое что
, такое что 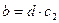 . Рассмотрим a+b=d·
. Рассмотрим a+b=d· 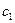 +d·
+d· 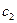 =d(
=d( 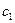 +
+ 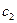 )=d·
)=d· 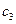 , где
, где 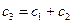 – целое число. Итак, a+b= d·
– целое число. Итак, a+b= d· 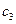 . Значит d|(a+b) (по определению). Аналогично доказывается, что d|(a-b).
. Значит d|(a+b) (по определению). Аналогично доказывается, что d|(a-b).
Дата добавления: 2015-08-01; просмотров: 656;
