Пример 2. Докажите, что если d|a и , то d|(a·c).

Докажите, что если d|a и 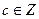, то d|(a·c).

Доказательство.

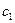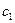Так как d|a, то существует целое число m такое, что a=d·m. Рассмотрим a·c=(d·m) ·c=d· (m·c)=d· , где – целое. Итак, a·c=d· 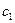, значит по определению d|(a·c).

Справедливы следующие теоремы.

Теорема 1.

Если a кратно m, m кратно b, то a кратно b.