А) Поле равномерно заряженной безграничной плоскости.

Бесконечная плоскость (рис.6) заряжена с постоянной плотностью ( 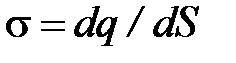- заряд приходящийся на единицу поверхности). Линии напряжен­ности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны.

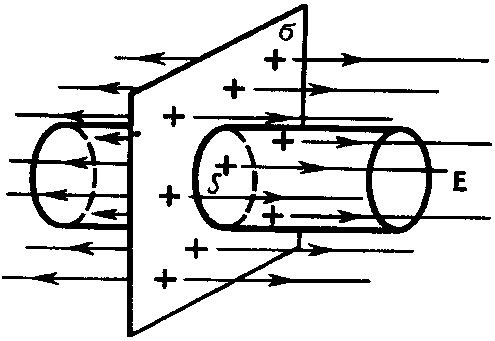
Рис.6

В качестве замкнутой поверхности выделим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллель­ны линиям напряженности (cos 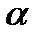=0), то поток вектора напряженности сквозь боковую по­верхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований рав­ны и для основания E 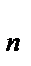, совпадает с Е), т. е. равен 2ES. Заряд, заключенный внутри ци­линдра, равен S. 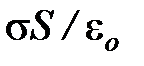Согласно теореме Гаусса , 2ES = , откуда

Е = 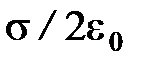. (7)

Из этой формулы вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.