В) Поле равномерно заряженной сферы

Сферическая поверхность радиуса R с общим зарядом q заряжена равномерно с поверхностной плотностью + . Благодаря равномерному распределению заряда по по­верхности поле, создаваемое им, обладает сфе­рической симметрией. Поэтому линии напря­женности направлены радиально (рис.8).

8 Рис.8

Вы­делим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r > R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по тео­реме Гаусса , 4nr 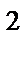E = Q/ 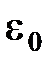, откуда

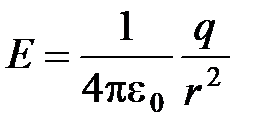(r R). (9)

Если r < R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверх­ности электростатическое поле отсутствует (Е = 0). Вне этой поверхности поле убывает с расстоянием r по такому же закону, как у точечного заряда.

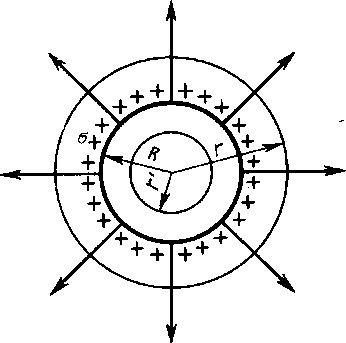
Г) Поле бесконеч­ной прямой нити (цилиндра)

Бесконечная нить радиуса R (рис. 9) заряжена равномерно с линейной плотностью ( 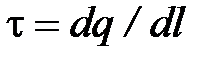- заряд приходящийся на единицу длины).

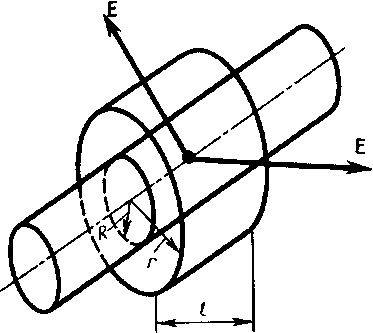
Рис.9

Из соображений сим­метрии следует, что линии напряженности бу­дут радиальными прямыми, перпендику­лярными поверхности нити. В качестве замкнутой поверхности выделим коаксиальный с заряженным цилиндр радиуса r и длиной l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую по­верхность 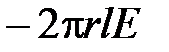. По теореме Гаусса при r > R 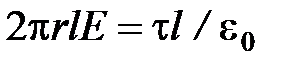, откуда

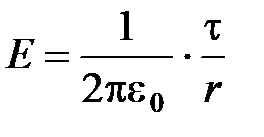(r > R). (10)

Если r < R,то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0. Таким образом, напряженность поля вне равномерно заряженного бесконечной нити определяется выражением (10), внутри же ее поле отсутствует.