Теорема Остро-градского-Гаусса и ее применение.

Поток вектора напряженности электростатического поля – число силовых линий пронизывающих площадку, перпендикулярную им (рис.5а).

Для однородного поля и плоской поверхности поток вектора напряженности сквозь площадку равен (рис.5б)

Ф_Е = ES cos α (5)

где α – угол между векторами Е и нормалью n к поверхности S.

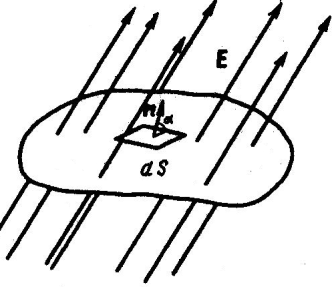
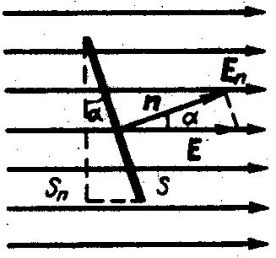
Рис.5а. Рис.5б.

Вычисление напряженности поля си­стемы электрических зарядов с помощью принципа суперпозиции электростатиче­ских полей можно значительно упростить, используя выведенную русским математиком М. В. Остроградским (1801—1862) а затем незави­симо от него применительно к электро­статическому полю немецким ученым К. Гауссом (1777-1855) теорему.

Теорема Остроградского Гаусса: поток вектора напряженности электрического поля в вакууме сквозь любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на электрическую постоянную

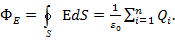(6)

Применение теоремы Остроградского-Гаусса для расчета электрического поля источников различной конфигурации: сферы, безграничной плоскости, бесконечной прямой нити.