Движение тел в жидкостях и газах. Число Рейнольдса.

При движении тела в жидкости или газе с небольшой скоростью сопротивление движению обусловлено силами трения и, как установил Стокс, пропорционально произведению вязкости среды на линейные размеры тела и первую степень скорости. Для тел шарообразной формы сопротивление вязкости равно

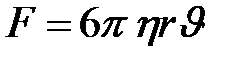
(10.8)

где 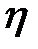- коэффициент вязкости, 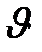- скорость и - радиус тела.

При больших скоростях движения сопротивление жидкости и газа обусловлено в основном затратой работы на образование вихрей. В этих случаях сопротивление (его часто называют лобовым сопротивлением) по закону Ньютона, пропорционально квадрату скорости движения и площади проекции тела на плоскость, перпендикулярную к направлению движения:

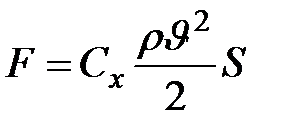
(10.9)

где 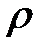- плотность среды, 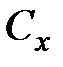- коэффициент лобового сопротивления (числовой коэффициент, различный для тел разных форм).

Форма тела может облегчать или же, наоборот, затруднять возникновение вихрей. Если тело имеет плавно обтекаемую форму, то разности давлений в различных участках его поверхности, вызванные различием скорости, будут незначительны; встречное движение слоев жидкости вблизи поверхности будет выражено слабо; срыва струй и завихрения жидкости почти не будет, и испытываемое телом сопротивление движению будет невелико. Напротив, если тело ограничено острыми углами, как, например, плоская пластинка, поставленная перпендикулярно к потоку, то разности давлений, вызванные изменением скорости при обтекании острых углов, будут большими, вихрей образуется много, и лобовое сопротивление окажется значительным.

На рис. 10.5 изображены тела различных размеров и форм, обладающие одним и тем же лобовым сопротивлением. Наиболее плавно обтекаемой оказывается вытянутая, каплеобразная форма, такая, какую придают всем фюзеляжам самолетов.

Тело подобной формы почти совсем не создает в потоке вихрей; сопротивление движению такого тела вызывается главным образом силами трения.

Опыт показывает, что формула (10.9) лобового сопротивления применима только в некоторых пределах значений скорости.

При малых скоростях (в воздухе до 1 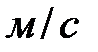), когда силы инерции малы в сравнении с силами внутреннего трения, сопротивление, в соответствии с законом Стокса, пропорционально не квадрату, а первой степени скорости. При больших скоростях (близких к скорости звука) сопротивление возрастает, по-видимому, пропорционально кубу скорости. При движении тела со скоростью, большей скорости звука, вновь оказывается справедливым закон квадрата скорости.

Таким образом, желая применять формулу (10.9) к любым скоростям движения, необходимо рассматривать коэффициент сопротивления 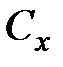как некоторую функцию коэффициента вязкости среды 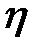, плотности среды 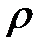, скорости движения 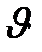и линейных размеров тела 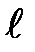. Можно совершенно строго доказать, что коэффициент сопротивления 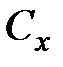зависит только от численной величины отношения 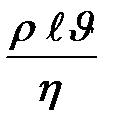. Нетрудно понять, что это именно так: коэффициент сопротивления 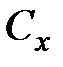является отвлеченным числом, поэтому функциональная зависимость его от величин должна сводиться к зависимости от такой комбинации этих величин, которая сама представляет собой отвлеченное число. Нетрудно убедиться, что отношение 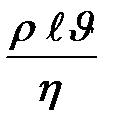как раз представляет собой отвлеченное число. Это соотношение:

(10.10)

называют числом Рейнольдса.

Итак, коэффициент лобового сопротивления представляет собой некоторую функцию чисел Рейнольдса:

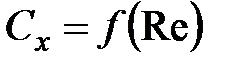
Отношение коэффициента вязкости к плотности среды 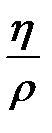называют кинематической вязкостью и обозначают буквой :

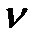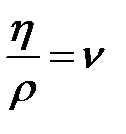
(10.11)

Из формулы (10.9) видно, что движение какого-либо определенного тела с определенной скоростью в различных средах сопровождается одинаковым лобовым сопротивлением, если равны кинематические вязкости этих сред. Иными словами, уменьшение коэффициента вязкости среды в 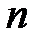раз при одновременном уменьшении плотности среды в 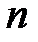раз не изменяет величины лобового сопротивления. Поэтому числа Рейнольдса обычно выражают не через коэффициент вязкости 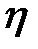, а через кинематическую вязкость :

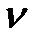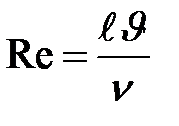
(10.12)

Нетрудно убедиться в том, что число Рейнольдса пропорционально отношению сил инерции 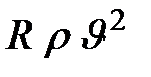к силам вязкости, действующим на поверхность тела, ; .

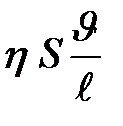Для малых чисел Рейнольдса коэффициент лобового сопротивления 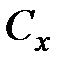по закону Стокса при увеличении 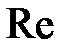убывает. При дальнейшем возрастании числа Рейнольдса уменьшение коэффициента лобового сопротивления все более замедляется в связи с проявлением инерции среды. В области чисел Рейнольдса порядка десятков тысяч ( 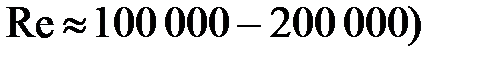коэффициент лобового сопротивления остается примерно постоянным.

В определенной области чисел Рейнольдса (для шара при Re от 200 000 до 300 000; для цилиндра при Re от 400 000 до 500 000) вдруг наступает резкое уменьшение коэффициента лобового сопротивления. Коэффициент лобового сопротивления уменьшается в три, четыре, пять раз, а затем при дальнейшем увеличении числа Рейнольдса вновь остается почти постоянным. Лобовое сопротивление в целом испытывает при этом также резкое уменьшение. Указанное явление носит название кризиса.

Кризис связан с резким изменением характера течения в слое жидкости (или газа), который прилегает к поверхности движущегося тела. Как известно, в определенном месте движущегося тела происходит «срыв вихрей». До этого места обтекание является ламинарным. При кризисе оно превращается в турбулентное; в связи с этим место срыва вихрей смещается назад, и лобовое сопротивление резко уменьшается.