Вязкость и течение жидкости при трении.
Чтобы установить меру вязкости, представим себе следующий опыт: возьмем две пластинки, смоченные какой-либо жидкостью (рис.10.1), и станем перемещать верхнюю пластинку относительно нижней в направлении, указанном стрелкой.
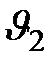
|

|
|
| Рис. 10.1 |
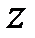
|
Слои жидкости, непосредственно соприкасающиеся с этими пластинками, прилипают к ним, все же остальные слои перемещаются, скользят друг по другу со скоростью тем большей, чем больше их расстояние от пластинок. Вязкость жидкости сказывается в том, что возникает сила, препятствующая перемещению слоев жидкости, а значит, и пластинок.
Проведем ось  перпендикулярно к слоям (а значит, и к скоростям движения слоев). Производная
перпендикулярно к слоям (а значит, и к скоростям движения слоев). Производная  от скорости слоев называется градиентом скорости. Если скорость слоев равномерно возрастает с увеличением координаты
от скорости слоев называется градиентом скорости. Если скорость слоев равномерно возрастает с увеличением координаты 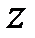 , то градиент скорости является постоянной для всей массы жидкости или газа и может быть выражен также через
, то градиент скорости является постоянной для всей массы жидкости или газа и может быть выражен также через 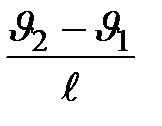 , где
, где 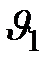 и
и 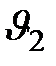 - скорости перемещения каких-нибудь двух тонких слоев,
- скорости перемещения каких-нибудь двух тонких слоев, 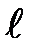 - их расстояние друг от друга.
- их расстояние друг от друга.
Ньютон установил для силы вязкости 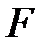 следующий закон:
следующий закон:
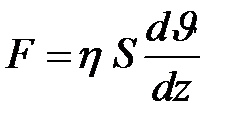
| (10.1) |
Он нам уже известен из § 8. Сила вязкости стремится остановить тот из двух смежных слоев, который движется быстрее, и ускорить тот, который движется медленнее.
При течении жидкости по трубе часть ее энергии расходуется на работу против сил трения и превращается в энергию молекулярно-теплового движения. Поэтому можно написать, приняв во внимание сказанное в § 9 п. 9.3:
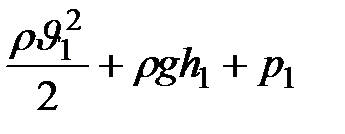 = = 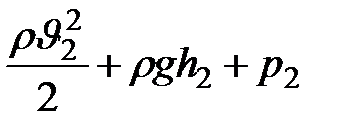 = = 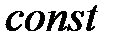 =
= =
= 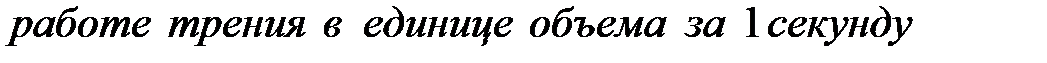
| (10.2) |
Течение при трении бывает или слоистым – ламинарным (от лат. 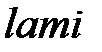
 - пластинка), или турбулентным (от лат.
- пластинка), или турбулентным (от лат.  - неспокойный).
- неспокойный).
При ламинарном течении слои жидкости скользят друг по другу со скоростями, увеличивающимися по мере удаления от стенок сосуда. Особенно удобно наблюдать ламинарное течение в узкой стеклянной трубке (рис. 10.2, а). Пока течение имеет слоистый характер, струя краски, пущенная в трубку, остается резко ограниченной. При увеличении скорости наступает такой момент, когда течение переходит в турбулентное: резкая граница между чистой и подкрашенной жидкостью исчезает, и вся трубка оказывается заполненной неправильными вихревыми движениями (рис. 10.2, б).
Скорость, при которой ламинарное течение превращается в турбулентное, называют критической скоростью.
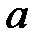
|
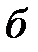
|
| Рис. 10.2 |
При установившемся течении жидкости по горизонтальной трубе, имеющей одинаковое сечение по всей длине, скорость будет наибольшей в тех точках поперечного сечения потока, которые наиболее удалены от стенок трубы. Частицы жидкости, непосредственно прилегающие к стенкам трубы, остаются неподвижными. На рис. 10.3 показано распределение скорости в трубе при ламинарном течении. Если радиус трубы 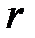 , то скорость
, то скорость 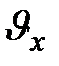 на расстоянии
на расстоянии 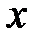 от центра поперечного сечения трубы равна:
от центра поперечного сечения трубы равна:
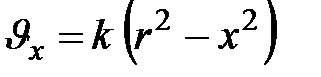
| (10.3) |
Где  - коэффициент пропорциональности, зависящий от падения давления на единицу длины трубы и от вязкости жидкости
- коэффициент пропорциональности, зависящий от падения давления на единицу длины трубы и от вязкости жидкости 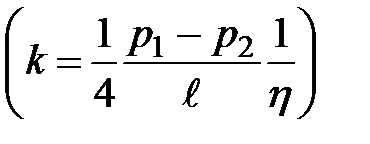 . Уравнение (10.3) представляет собой уравнение параболы, которая на рис. 10.3 изображена пунктиром; поэтому говорят, что скорости ламинарного течения в трубе распределены по параболическому закону.
. Уравнение (10.3) представляет собой уравнение параболы, которая на рис. 10.3 изображена пунктиром; поэтому говорят, что скорости ламинарного течения в трубе распределены по параболическому закону.
| Рис. 10.3 |
При турбулентном течении (рис. 10.4) скорость течения пропорциональна примерно корню седьмой степени из расстояния от стенки (при шероховатых стенках степень корня ниже):
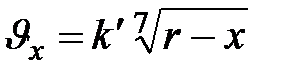
| (10.4) |
Слой жидкости, непосредственно прилегающий к стенкам, и при турбулентном течении остается неподвижным: в смежном тонком слое сохраняется ламинарное течение жидкости.
| Рис. 10.4 |
Практически важной является средняя скорость 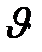 течения жидкости по трубе. Очевидно, что количество жидкости
течения жидкости по трубе. Очевидно, что количество жидкости 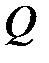 , протекающей за 1 секунду через поперечное сечение трубы
, протекающей за 1 секунду через поперечное сечение трубы  , равно произведению средней скорости течения на площадь поперечного сечения:
, равно произведению средней скорости течения на площадь поперечного сечения: 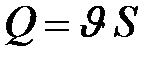 .
.
Экспериментально изучая скорость течения жидкостей по трубам, Гаген и независимо от него Пуазель нашли, что средняя скорость ламинарного течения жидкости по трубе пропорциональна падению давления на единицу длины трубы, пропорциональна квадрату радиуса трубы и обратно пропорциональна коэффициенту вязкости:
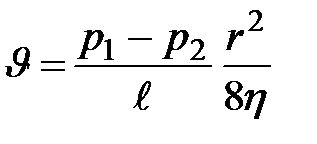
| (10.5) |
Поскольку 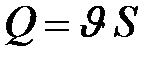 , а для круглой трубы
, а для круглой трубы  , то нетрудно заметить, что закон Гагена-Пуазеля можно переписать так:
, то нетрудно заметить, что закон Гагена-Пуазеля можно переписать так:
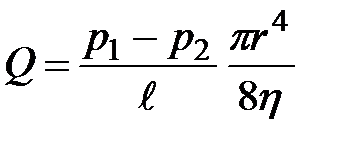
| (10.6) |
При турбулентном течении скорость течения пропорциональна корню квадратному из падения давления:

| (10.7) |
Выражение (10.7) – это формула Шези, где 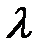 - коэффициент сопротивления течению жидкости. Формула Шези применима для труб любого сечения.
- коэффициент сопротивления течению жидкости. Формула Шези применима для труб любого сечения.
Иногда пользуются формулой Шези не только для турбулентного, но также и для ламинарного течения. Это допустимо, если считать, что для ламинарного течения коэффициент сопротивления течению 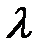 равен:
равен:
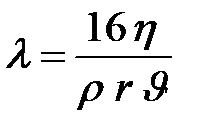
|
Нетрудно убедиться, что подстановка этого выражения для 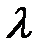 в формулу (10.7) превращает формулу Шези с закон Пуазеля. Следовательно, для ламинарного течения коэффициент сопротивления убывает с увеличением скорости; для турбулентного течения
в формулу (10.7) превращает формулу Шези с закон Пуазеля. Следовательно, для ламинарного течения коэффициент сопротивления убывает с увеличением скорости; для турбулентного течения 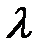 почти не зависит от скорости.
почти не зависит от скорости.
Дата добавления: 2015-08-11; просмотров: 1238;
