Уравнение Бернулли для несжимаемой жидкости
Рассмотрим установившееся (стационарное) точение идеальной (без трения) жидкости в трубке тока. Поперечное сечение трубки тока в различных местах может быть неодинаковым, и в соответствии с этим меняется скорость течения. Струя жидкости нигде не претерпевает разрыва. Из этого условия неразрывности струи следует, что произведение скорости несжимаемой и невязкой жидкости на поперечное сечение трубки тока есть величина постоянная.
Пусть за время 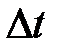 масса жидкости
масса жидкости 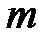 втекает в один конец выделенной части трубки через сечение
втекает в один конец выделенной части трубки через сечение 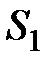 , где скорость
, где скорость 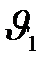 и давление
и давление 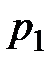 (рис. 9.5). За это же время
(рис. 9.5). За это же время 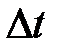 через другое сечение трубки тока
через другое сечение трубки тока  , где скорость жидкости равна
, где скорость жидкости равна 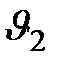 и давление
и давление 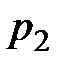 , вытекает такая же масса жидкости
, вытекает такая же масса жидкости 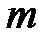 . При установившемся (стационарном) течении в выделенной части трубки не происходит ни накапливания, ни расходования энергии. Следовательно, энергия, передаваемая за время
. При установившемся (стационарном) течении в выделенной части трубки не происходит ни накапливания, ни расходования энергии. Следовательно, энергия, передаваемая за время 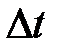 через сечение
через сечение 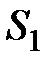 , должна быть равна энергии, передаваемой за то же время через сечение
, должна быть равна энергии, передаваемой за то же время через сечение  . За время
. За время 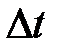 через сечение
через сечение 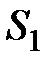 проходит масса жидкости
проходит масса жидкости 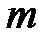 . Ее кинетическая энергия равна
. Ее кинетическая энергия равна 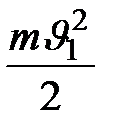 и потенциальная энергия тяжести равна
и потенциальная энергия тяжести равна 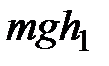 (где
(где 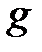 - ускорение силы тяжести и
- ускорение силы тяжести и 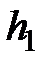 - высота центра тяжести сечения
- высота центра тяжести сечения 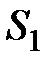 над некоторым уровнем, например, уровнем моря).
над некоторым уровнем, например, уровнем моря).
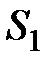
|

|
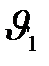
|
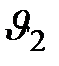
|
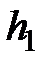
|
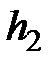
|
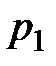
|
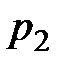
|
| Рис. 9.5 |
Следовательно, за время 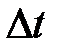 через сечение
через сечение 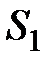 конвекционно передается энергия
конвекционно передается энергия
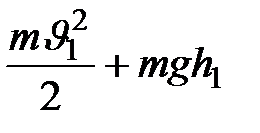 
|
Однако, кроме конвекционной передачи энергии, в данном случае еще имеет место передача энергии тягой, а именно, жидкость, находящаяся позади, производит работу, направленную на продвижение жидкости, находящейся впереди. Энергия, передаваемая тягой за время 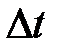 через сечение
через сечение 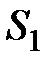 , равна, очевидно, работе, которую жидкость, находящаяся позади сечения
, равна, очевидно, работе, которую жидкость, находящаяся позади сечения 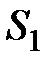 , производит за то же время
, производит за то же время 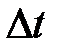 , т.е. рана произведению силы
, т.е. рана произведению силы 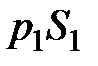 на путь
на путь 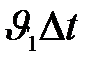 . Таким образом, энергия, передаваемая за время
. Таким образом, энергия, передаваемая за время 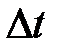 через сечение
через сечение 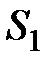 , состоит из трех слагаемых:
, состоит из трех слагаемых:
 
|
Согласно условию неразрывности струи объем жидкости, втекающей в трубку за время 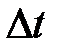 , т.е
, т.е 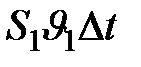 равен объему жидкости, вытекающей за тот же промежуток времени из трубки тока:
равен объему жидкости, вытекающей за тот же промежуток времени из трубки тока: 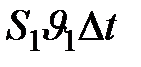 =
= 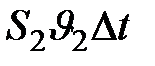 . Разделим обе части предыдущего уравнения на эти равные друг другу объемы, учтя, что масса жидкости, деленная на ее объем, представляет собой плотность жидкости, т.е
. Разделим обе части предыдущего уравнения на эти равные друг другу объемы, учтя, что масса жидкости, деленная на ее объем, представляет собой плотность жидкости, т.е 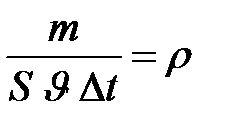 :
:
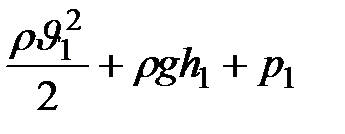 = = 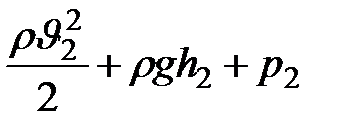
| (9.7) |
В этом уравнении 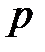 называется статическим давлением,
называется статическим давлением, 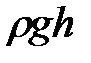 - гидравлическим давлением,
- гидравлическим давлением, 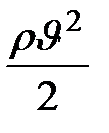 - динамическим давлением.
- динамическим давлением.
Уравнение (9.7) получено в 1738 году Бернулли и называется уравнением Бернулли.
В суженной части трубки тока скорость жидкости больше, чем в остальном потоке. Поступая в узкую часть трубки тока, жидкость двигается ускоренно; следовательно, на жидкость, втекающую в узкую часть трубки тока, действуют со стороны жидкости, еще находящейся в широкой части трубки, некоторая сила. Очевидно, что эта сила возникает вследствие разности статических давлений 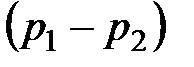 в широком и узком местах трубки. Сила направлена в сторону узкой части трубки; значит, в широких местах трубки давление больше, чем в узких. Иными словами, в местах сужения трубки тока давление понижено.
в широком и узком местах трубки. Сила направлена в сторону узкой части трубки; значит, в широких местах трубки давление больше, чем в узких. Иными словами, в местах сужения трубки тока давление понижено.
При горизонтальном течении жидкости сумма статического и динамического давлений остается величиной постоянной. Эту сумму называют полным давлением.
Статическое давление измеряют с помощью манометра, неподвижного относительно текущей жидкости. Практически бывает достаточно взять манометр, плоскость отверстия которого расположена параллельно линиям тока (трубка  на рис. 9.6).
на рис. 9.6).
Полное давление измеряют манометром, отверстие которого расположено перпендикулярно к линиям тока (трубка 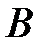 на рис. 9.6); попав в отверстие, жидкость «теряет» свою скорость. Динамическое давление в этой трубке будет равно нулю, оставшееся статическое давление будет равно сумме статического и динамического давлений текущей жидкости, следовательно, манометр покажет полное давление.
на рис. 9.6); попав в отверстие, жидкость «теряет» свою скорость. Динамическое давление в этой трубке будет равно нулю, оставшееся статическое давление будет равно сумме статического и динамического давлений текущей жидкости, следовательно, манометр покажет полное давление.

|
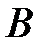
|

|

|
| Рис. 9.6 |
Изображенная на рис. 9.6 трубка 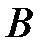 носит название трубки Пито.
носит название трубки Пито.
Уравнение Бернулли было выведено в предположении, что сумма кинетической энергии и потенциальной энергии тяжести текущей жидкости остается неизменной. В действительности же некоторая часть указанной энергии расходуется на работу, направленную против сил трения. В связи с этим жидкость нагревается, и энергия молекулярно-теплового движения жидкости, которую мы считали постоянной и поэтому не учитывали, возрастает. Мы предполагали также, что частицы жидкости не проходят сквозь боковую поверхность трубки тока. В действительности же тепловое движение нарушает течение жидкости по определенным линиям тока.
Поэтому к весьма вязким жидкостям уравнение Бернулли неприменимо. Но для таких жидкостей, как вода, а также для воздуха уравнение Бернулли практически является достаточно точным.
При горизонтальном течении сумма статического и динамического давлений остается постоянной величиной, поэтому в струе статическое давление всегда бывает меньше, чем в неподвижной жидкости, и при больших скоростях может стать даже отрицательным. В этом случае жидкость, протекающая по узкой части трубы, будет находиться в состоянии всестороннего растяжения, а так как прочность жидкости на разрыв велика, то отрицательное давление может достигнуть значительной величины. Однако, когда давление падает до нуля, обычно происходит разрыв жидкости – это так называемое явление кавитации. При кавитации происходит интенсивное перемешивание жидкости, что приводит к резкой потере скорости течения жидкости – возникает гидравлический удар, сопровождающийся сильным шумом, а при определенных условиях и к разрыву трубы.
Если давление в широкой части трубы равно атмосферному, то давление в узкой части трубы будет меньше атмосферного. На этом явлении основано действие ряда приборов, например, инжектора, водоструйных насосов, карбюратора.
Дата добавления: 2015-08-11; просмотров: 1362;
