Явления переноса в газах. Опытные законы явлений переноса.
В равновесном состоянии газа все его параметры (температура, давление, плотность и др.) одинаковы во всех точках занимаемого объема. Рассмотрим теперь явления, возникающие при отклонении газа от равновесия. Наука, изучающая процессы, возникающие при нарушениях равновесия, называется физической кинетикой.
Если систему вывести из равновесия, то возникнут пространственные неоднородности физических величин (неоднородность плотности, температуры и т.д.), обусловливающие потоки или массы, или импульса, или энергии и др., которые возвратят систему в равновесие. Соответствующие процессы называют явлениями переноса. К ним относятся диффузия, внутреннее трение (или вязкость), теплопроводность. Общим для всех явлений является то, что они возникают в газах в результате нарушения хаотичности движения молекул. Эти нарушения вызваны направленным воздействием на газ в случае диффузии должна быть создана неоднородность плотности, в случае теплопроводности – неоднородность температуры, в случае внутреннего трения – неодинаковость скоростей направленного движения молекул в разных слоях газа.
В рассматриваемых явлениях наблюдается направленный перенос какой-либо величины. Потоком переносимой физической величины через поверхность  называется количество этой величины, происходящее в единицу времени через эту поверхность. Поток является скалярной алгебраической величиной. Знак потока определяется выбором положительного направления (например, направлением оси, вдоль которой распространяется поток).
называется количество этой величины, происходящее в единицу времени через эту поверхность. Поток является скалярной алгебраической величиной. Знак потока определяется выбором положительного направления (например, направлением оси, вдоль которой распространяется поток).
Рассмотрим законы явлений переноса, установленные опытным путем.
1. Диффузия.
Если в разных местах объема, в котором находится газ, концентрация молекул (или плотность) разная, то за счет хаотичного движения молекул произойдет выравнивание концентраций (или плотностей).
Диффузия – это явление переноса частиц вещества, а, следовательно, и массы, из области, где плотность вещества больше, в область, где плотность меньше. Пусть в направлении оси 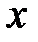 по обе стороны от площади
по обе стороны от площади  , перпендикулярной оси
, перпендикулярной оси 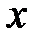 , концентрации молекул одинаковы (рис. 8.4), одинаковой будет и плотность вещества:
, концентрации молекул одинаковы (рис. 8.4), одинаковой будет и плотность вещества:
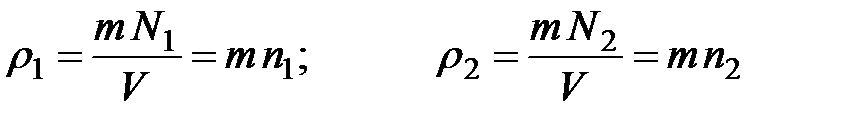 , ,
|
|
где 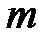 - масса одной молекулы.
- масса одной молекулы.
Пусть 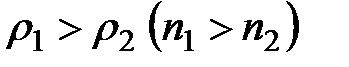 . Быстроту изменения плотности в направлении оси
. Быстроту изменения плотности в направлении оси 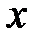 выразим через градиент плотности
выразим через градиент плотности  . Тогда диффузионный поток массы вещества через площадь
. Тогда диффузионный поток массы вещества через площадь  , перпендикулярную направлению переноса, будет определяться выражением
, перпендикулярную направлению переноса, будет определяться выражением
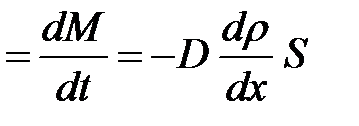
| (8.3)
|
это закон Фика.
Здесь 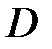 - коэффициент диффузии – физическая величина, численно равная потоку массы вещества, проходящему через единичную площадь, перпендикулярную оси
- коэффициент диффузии – физическая величина, численно равная потоку массы вещества, проходящему через единичную площадь, перпендикулярную оси 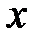 , при градиенте плотности, равном единице. Измеряется коэффициент диффузии в
, при градиенте плотности, равном единице. Измеряется коэффициент диффузии в 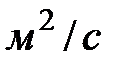 , зависит от природы вещества и внешних условий, в которых находится газ. Знак минус в формуле (8.3) указывает на то, что перенос массы происходит оттуда, где плотность больше, туда, где плотность вещества меньше, т.е. противоположно градиенту плотности.
, зависит от природы вещества и внешних условий, в которых находится газ. Знак минус в формуле (8.3) указывает на то, что перенос массы происходит оттуда, где плотность больше, туда, где плотность вещества меньше, т.е. противоположно градиенту плотности.
2. Теплопроводность.
Теплопроводностью называется явление переноса энергии в форме тепла из области, где температура выше, в область, где температура ниже (рис. 8.5). Быстрота изменения температуры вдоль оси 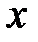 определяется градиентом температуры
определяется градиентом температуры 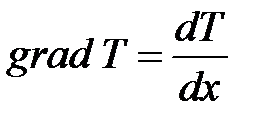 . Градиент температуры приводит к возникновению теплового потока.
. Градиент температуры приводит к возникновению теплового потока.
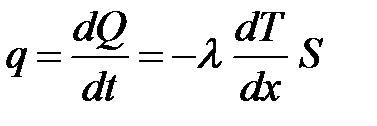
| (8.4)
|
- это закон Фурье
Здесь 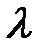 - коэффициент теплопроводности – физическая величина, численно равная потоку теплоты, проходящему через единицу площади, перпендикулярной оси
- коэффициент теплопроводности – физическая величина, численно равная потоку теплоты, проходящему через единицу площади, перпендикулярной оси  , при градиенте температуры, равном единице. Коэффициент теплопроводности имеет размерность
, при градиенте температуры, равном единице. Коэффициент теплопроводности имеет размерность  , зависит от природы газа и внешних условий, в которых находится газ. Знак минус в формуле (8.4) указывает на то, что тепловой поток направлен в сторону уменьшения температуры, т.е. противоположно градиенту температуры.
, зависит от природы газа и внешних условий, в которых находится газ. Знак минус в формуле (8.4) указывает на то, что тепловой поток направлен в сторону уменьшения температуры, т.е. противоположно градиенту температуры.
3. Внутреннее трение или вязкость.
Рассмотрим поток газа, скорость течения в котором различна в разных местах. Это можно осуществить, например, если в газе параллельно вертикальной оси (рис.8.6) перемещать с постоянной скоростью 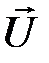 пластину.
пластину.
Тогда слой газа, прилегающий к пластине, будет двигаться со скоростью этой пластины; следующие слои газа из-за трения между ними будут двигаться со все меньшей скоростью. Таким образом, вдоль оси 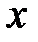 скорость слоев газа будет уменьшаться, значит, вдоль оси
скорость слоев газа будет уменьшаться, значит, вдоль оси 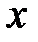 имеется градиент скорости
имеется градиент скорости
Вместе со скоростью вдоль оси 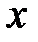 при переходе от слоя к слою будет изменяться и импульс молекул
при переходе от слоя к слою будет изменяться и импульс молекул 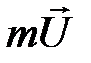 . Двигаясь хаотично, молекулы будут переходить из одного слоя в другой. При переходе молекулы из быстрого слоя в более медленный она будет отдавать часть импульса своего упорядоченного движения молекулам этого слоя и ускорять их. Наоборот, пр и переходе молекулы из медленного слоя в более быстрый слой она будет его замедлять. Поэтому, если в газе провести площадку
. Двигаясь хаотично, молекулы будут переходить из одного слоя в другой. При переходе молекулы из быстрого слоя в более медленный она будет отдавать часть импульса своего упорядоченного движения молекулам этого слоя и ускорять их. Наоборот, пр и переходе молекулы из медленного слоя в более быстрый слой она будет его замедлять. Поэтому, если в газе провести площадку 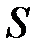 , перпендикулярную оси
, перпендикулярную оси 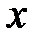 , то через нее слева направо будут проходить молекулы, имеющие больший импульс
, то через нее слева направо будут проходить молекулы, имеющие больший импульс 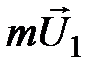 упорядоченного движения, чем импульс
упорядоченного движения, чем импульс 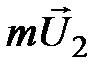 молекул, переходящих справа налево. Явление, связанное с переносом количества упорядоченного движения молекул вещества, т.е. переносом импульса, называется вязкостью или внутренним трением.Возникает поток импульса в направлении, противоположном градиенту скорости. В соответствии со вторым законом Ньютона изменение импульса за единицу времени равно действующей на тело силе. В данном случае это будет сила внутреннего трения. На опыте установлено, что сила внутреннего трения, возникающая на границе двух движущихся относительно друг друга слоев площадью
молекул, переходящих справа налево. Явление, связанное с переносом количества упорядоченного движения молекул вещества, т.е. переносом импульса, называется вязкостью или внутренним трением.Возникает поток импульса в направлении, противоположном градиенту скорости. В соответствии со вторым законом Ньютона изменение импульса за единицу времени равно действующей на тело силе. В данном случае это будет сила внутреннего трения. На опыте установлено, что сила внутреннего трения, возникающая на границе двух движущихся относительно друг друга слоев площадью  , равна
, равна
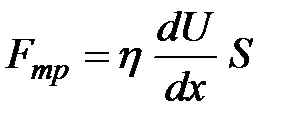 - -
| (8.5)
|
это закон Ньютона
Здесь 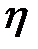 - коэффициент вязкости (или коэффициент внутреннего трения) – физическая величина, численно равная силе внутреннего рения, возникающей при движении соприкасающихся слоев газа единичной площади при градиенте скорости, равном единице. Коэффициент вязкости имеет размерность
- коэффициент вязкости (или коэффициент внутреннего трения) – физическая величина, численно равная силе внутреннего рения, возникающей при движении соприкасающихся слоев газа единичной площади при градиенте скорости, равном единице. Коэффициент вязкости имеет размерность 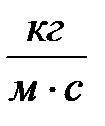 и зависит от природы газа и его температуры.
и зависит от природы газа и его температуры.
Дата добавления: 2015-08-11; просмотров: 3521;
 называется количество этой величины, происходящее в единицу времени через эту поверхность. Поток является скалярной алгебраической величиной. Знак потока определяется выбором положительного направления (например, направлением оси, вдоль которой распространяется поток).
называется количество этой величины, происходящее в единицу времени через эту поверхность. Поток является скалярной алгебраической величиной. Знак потока определяется выбором положительного направления (например, направлением оси, вдоль которой распространяется поток). по обе стороны от площади
по обе стороны от площади  , перпендикулярной оси
, перпендикулярной оси  , концентрации молекул одинаковы (рис. 8.4), одинаковой будет и плотность вещества:
, концентрации молекул одинаковы (рис. 8.4), одинаковой будет и плотность вещества: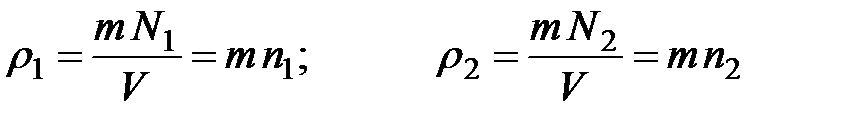 ,
,
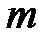 - масса одной молекулы.
- масса одной молекулы.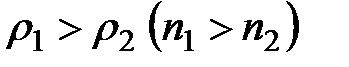 . Быстроту изменения плотности в направлении оси
. Быстроту изменения плотности в направлении оси 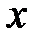 выразим через градиент плотности
выразим через градиент плотности  . Тогда диффузионный поток массы вещества через площадь
. Тогда диффузионный поток массы вещества через площадь  , перпендикулярную направлению переноса, будет определяться выражением
, перпендикулярную направлению переноса, будет определяться выражением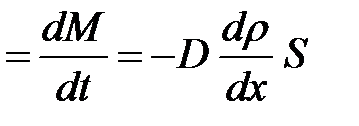
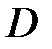 - коэффициент диффузии – физическая величина, численно равная потоку массы вещества, проходящему через единичную площадь, перпендикулярную оси
- коэффициент диффузии – физическая величина, численно равная потоку массы вещества, проходящему через единичную площадь, перпендикулярную оси 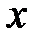 , при градиенте плотности, равном единице. Измеряется коэффициент диффузии в
, при градиенте плотности, равном единице. Измеряется коэффициент диффузии в 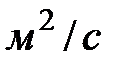 , зависит от природы вещества и внешних условий, в которых находится газ. Знак минус в формуле (8.3) указывает на то, что перенос массы происходит оттуда, где плотность больше, туда, где плотность вещества меньше, т.е. противоположно градиенту плотности.
, зависит от природы вещества и внешних условий, в которых находится газ. Знак минус в формуле (8.3) указывает на то, что перенос массы происходит оттуда, где плотность больше, туда, где плотность вещества меньше, т.е. противоположно градиенту плотности.
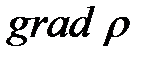
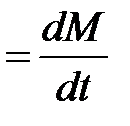
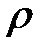

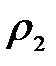


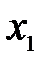
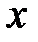 определяется градиентом температуры
определяется градиентом температуры 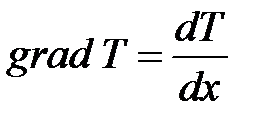 . Градиент температуры приводит к возникновению теплового потока.
. Градиент температуры приводит к возникновению теплового потока.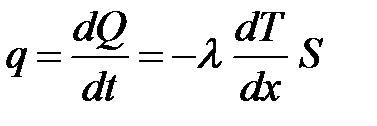
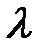 - коэффициент теплопроводности – физическая величина, численно равная потоку теплоты, проходящему через единицу площади, перпендикулярной оси
- коэффициент теплопроводности – физическая величина, численно равная потоку теплоты, проходящему через единицу площади, перпендикулярной оси  , при градиенте температуры, равном единице. Коэффициент теплопроводности имеет размерность
, при градиенте температуры, равном единице. Коэффициент теплопроводности имеет размерность  , зависит от природы газа и внешних условий, в которых находится газ. Знак минус в формуле (8.4) указывает на то, что тепловой поток направлен в сторону уменьшения температуры, т.е. противоположно градиенту температуры.
, зависит от природы газа и внешних условий, в которых находится газ. Знак минус в формуле (8.4) указывает на то, что тепловой поток направлен в сторону уменьшения температуры, т.е. противоположно градиенту температуры.
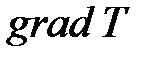
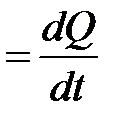
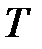
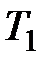



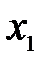

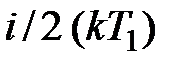

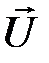 пластину.
пластину.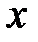 скорость слоев газа будет уменьшаться, значит, вдоль оси
скорость слоев газа будет уменьшаться, значит, вдоль оси 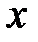 имеется градиент скорости
имеется градиент скорости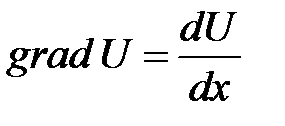
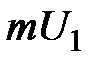
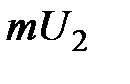
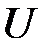
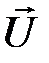
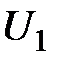

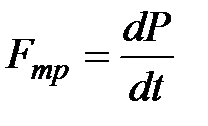
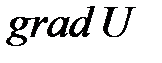
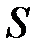
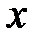
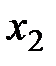
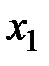
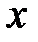 при переходе от слоя к слою будет изменяться и импульс молекул
при переходе от слоя к слою будет изменяться и импульс молекул 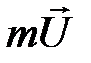 . Двигаясь хаотично, молекулы будут переходить из одного слоя в другой. При переходе молекулы из быстрого слоя в более медленный она будет отдавать часть импульса своего упорядоченного движения молекулам этого слоя и ускорять их. Наоборот, пр и переходе молекулы из медленного слоя в более быстрый слой она будет его замедлять. Поэтому, если в газе провести площадку
. Двигаясь хаотично, молекулы будут переходить из одного слоя в другой. При переходе молекулы из быстрого слоя в более медленный она будет отдавать часть импульса своего упорядоченного движения молекулам этого слоя и ускорять их. Наоборот, пр и переходе молекулы из медленного слоя в более быстрый слой она будет его замедлять. Поэтому, если в газе провести площадку 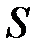 , перпендикулярную оси
, перпендикулярную оси 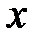 , то через нее слева направо будут проходить молекулы, имеющие больший импульс
, то через нее слева направо будут проходить молекулы, имеющие больший импульс 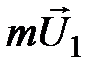 упорядоченного движения, чем импульс
упорядоченного движения, чем импульс 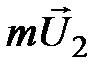 молекул, переходящих справа налево. Явление, связанное с переносом количества упорядоченного движения молекул вещества, т.е. переносом импульса, называется вязкостью или внутренним трением.Возникает поток импульса в направлении, противоположном градиенту скорости. В соответствии со вторым законом Ньютона изменение импульса за единицу времени равно действующей на тело силе. В данном случае это будет сила внутреннего трения. На опыте установлено, что сила внутреннего трения, возникающая на границе двух движущихся относительно друг друга слоев площадью
молекул, переходящих справа налево. Явление, связанное с переносом количества упорядоченного движения молекул вещества, т.е. переносом импульса, называется вязкостью или внутренним трением.Возникает поток импульса в направлении, противоположном градиенту скорости. В соответствии со вторым законом Ньютона изменение импульса за единицу времени равно действующей на тело силе. В данном случае это будет сила внутреннего трения. На опыте установлено, что сила внутреннего трения, возникающая на границе двух движущихся относительно друг друга слоев площадью  , равна
, равна
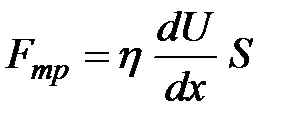 -
-
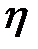 - коэффициент вязкости (или коэффициент внутреннего трения) – физическая величина, численно равная силе внутреннего рения, возникающей при движении соприкасающихся слоев газа единичной площади при градиенте скорости, равном единице. Коэффициент вязкости имеет размерность
- коэффициент вязкости (или коэффициент внутреннего трения) – физическая величина, численно равная силе внутреннего рения, возникающей при движении соприкасающихся слоев газа единичной площади при градиенте скорости, равном единице. Коэффициент вязкости имеет размерность 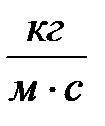 и зависит от природы газа и его температуры.
и зависит от природы газа и его температуры.