Адиабатное течение газа
В технической газодинамике весьма важным случаем является течение газа по трубопроводу переменного сечения без притока или отдачи тепла и без производства работы. В этом случае, когда 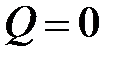 и
и 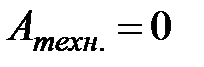 (для упрощения положим, что и
(для упрощения положим, что и 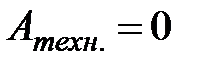 ), основное уравнение газодинамики преобразуется в уравнение, которое является термодинамическим обобщением уравнения Бернулли:
), основное уравнение газодинамики преобразуется в уравнение, которое является термодинамическим обобщением уравнения Бернулли:
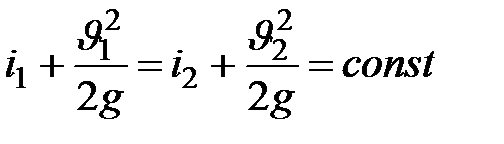
| (9.10) |
Здесь в отличие от уравнения Бернулли (9.7) вместо давления, деленного на плотность фигурирует теплосодержание; но 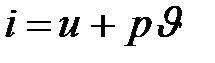 , и очевидно, что для потока несжимаемой жидкости, когда нет необходимости учитывать изменение термодинамического состояния (т.е. когда внутренняя энергия жидкости предполагается постоянной и плотность неизменна), уравнение (9.10) переходит в уравнение Бернулли.
, и очевидно, что для потока несжимаемой жидкости, когда нет необходимости учитывать изменение термодинамического состояния (т.е. когда внутренняя энергия жидкости предполагается постоянной и плотность неизменна), уравнение (9.10) переходит в уравнение Бернулли.
Из термодинамического обобщения уравнения Бернулли мы видим, что сумма теплосодержания и кинетической энергии газового потока при стационарном адиабатном течении без производства работы одинакова для всех сечений потока.
Течение, при котором скорость газа убывает, а плотность, давление и температура растут, называется течением со сжатием. Следует подчеркнуть, что здесь слово «сжатие» относится к термодинамическому состоянию потока, к отдельному объему газа, а отнюдь не к площади поперечного сечения трубопровода; при не слишком больших начальных скоростях газа в расширяющемся трубопроводе газ затормаживается, кинетическая энергия его уменьшается, а температура и плотность растут, т.е. имеет место течение со сжатием.
Течение, при котором кинетическая энергия потока растет, а плотность, давление и температура уменьшаются, называется течением с расширением. Рассмотрим оба случая течения в отдельности.
Течение с расширением имеет место, например, при истечении газа из камеры реактивного двигателя.
При адиабатном течении с расширением прирост кинетической энергии 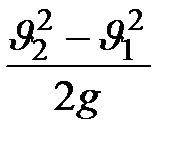 вызывается убылью теплосодержания
вызывается убылью теплосодержания 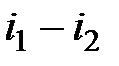 и падением температуры:
и падением температуры:
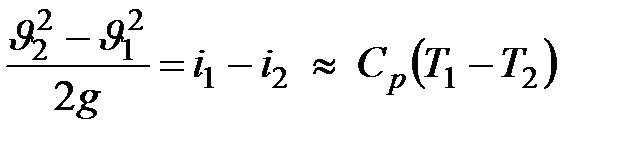
| (9.11) |
Падение температуры сопровождается уменьшением давления 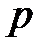 и плотности газа
и плотности газа 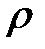 ; когда расширение газа происходит равновесно, можно воспользоваться уравнением Пуассона
; когда расширение газа происходит равновесно, можно воспользоваться уравнением Пуассона
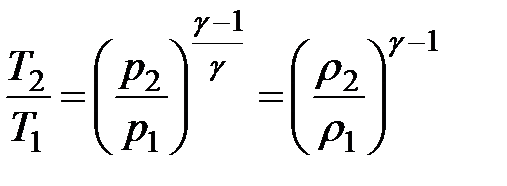
|
Следовательно,
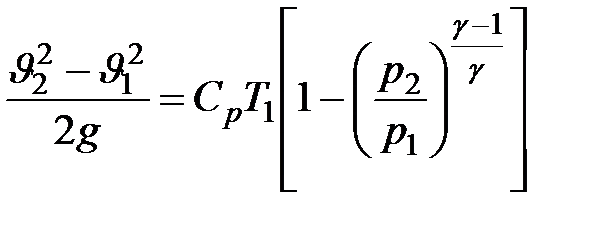
| (9.12) |
Здесь согласно уравнению Майера 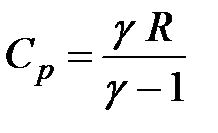 .
.
Пусть из баллона, где давление газа 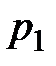 и температура
и температура 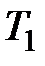 , газ адиабатно вытекает через отверстие площадью
, газ адиабатно вытекает через отверстие площадью  в резервуар, в котором давление («противодавление»)
в резервуар, в котором давление («противодавление») 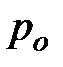 . При небольших перепадах давления (когда
. При небольших перепадах давления (когда 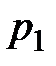 превышает
превышает 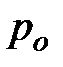 не более чем в 1,8-1,9 раза), давление газа в вытекающей струе
не более чем в 1,8-1,9 раза), давление газа в вытекающей струе 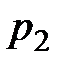 равно противодавлению
равно противодавлению 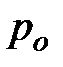 . В этом случае согласно уравнению (9.12) скорость истечения определяется формулой:
. В этом случае согласно уравнению (9.12) скорость истечения определяется формулой:
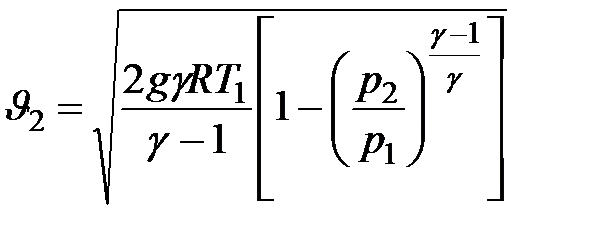
| (9.13) |
Здесь 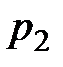 - статическое давление в вытекающей струе.
- статическое давление в вытекающей струе.
Весовой расход газа 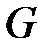 ( в
( в 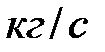 ) равен произведению площади поперечного сечения отверстия (в
) равен произведению площади поперечного сечения отверстия (в 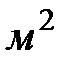 ) на скорость истечения (в
) на скорость истечения (в 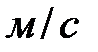 ) и на плотность вытекающего газа ( в
) и на плотность вытекающего газа ( в 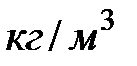 ):
):
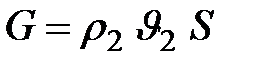
|
По мере уменьшения противодавления 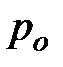 давление в вытекающей струе
давление в вытекающей струе 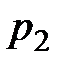 будет уменьшаться, а вместе с ним будет адиабатно уменьшаться по закону Пуассона и плотность вытекающего газа; скорость истечения будет расти.
будет уменьшаться, а вместе с ним будет адиабатно уменьшаться по закону Пуассона и плотность вытекающего газа; скорость истечения будет расти.
Весовой расход газа через данное отверстие  определяется двумя величинами: плотностью и скоростью истечения газа. Первая из этих величин,
определяется двумя величинами: плотностью и скоростью истечения газа. Первая из этих величин, 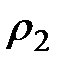 , с уменьшением
, с уменьшением 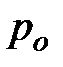 убывает, а вторая,
убывает, а вторая, 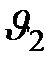 , наоборот, растет. Расход газа с уменьшением противодавления
, наоборот, растет. Расход газа с уменьшением противодавления 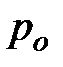 первое время увеличивается за счет быстрого увеличения скорости; затем расход замедляется за счет заметного уменьшения плотности и, наконец, становится постоянным: каким бы малым ни было противодавление, расход газа будет иметь одну и ту же величину.
первое время увеличивается за счет быстрого увеличения скорости; затем расход замедляется за счет заметного уменьшения плотности и, наконец, становится постоянным: каким бы малым ни было противодавление, расход газа будет иметь одну и ту же величину.
Таким образом, оказывается, что когда противодавление составляет примерно половину давления в баллоне, то дальнейшее уменьшение противодавления является бесполезным для повышения скорости истечения и расхода газа. В струе устанавливается некоторое критическое значение скорости истечения, давления, температуры и плотности газа, которые уже более не изменяются, как бы в дальнейшем не уменьшали противодавление. Если до этого момента давление на выходе в струе оставалось равным противодавлению 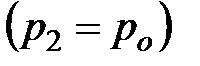 , то с указанного момента при истечении газа с критической скоростью у выходного отверстия устанавливается скачок давления
, то с указанного момента при истечении газа с критической скоростью у выходного отверстия устанавливается скачок давления 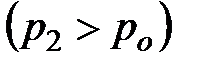 , так как уменьшение
, так как уменьшение 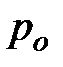 уже не будет больше вызывать уменьшения
уже не будет больше вызывать уменьшения 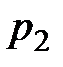 .
.
Скорость газа, вытекающего из отверстия или из сужающегося насадка, не может быть больше критической скорости:
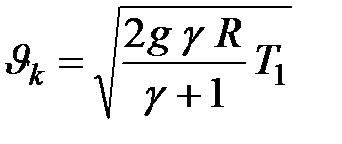
| (9.14) |
Понижение температуры в струе при критическом истечении согласно уравнению Пуассона и формуле (9.13) равно:
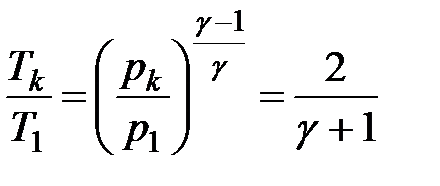
|
Таким образом, 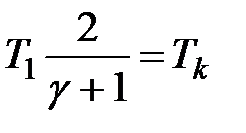 , и, стало быть, формулу (9.14) можно переписать так:
, и, стало быть, формулу (9.14) можно переписать так:
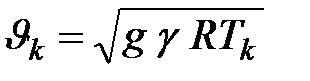
|
Критическая скорость равна скорости, с которой распространяется звук при имеющейся в струе температуре 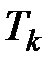 . Ни при каком сколь угодно большом давлении в баллоне газ не может вытекать из отверстия со скоростью, большей, чем скорость звука.
. Ни при каком сколь угодно большом давлении в баллоне газ не может вытекать из отверстия со скоростью, большей, чем скорость звука.
Максимальный расход газа при критическом течении определяется формулой
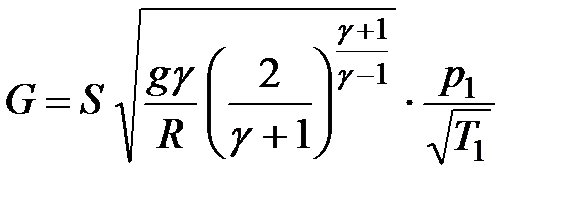
|
Чтобы понять физические причины, обуславливающие существование критических параметров в струе вытекающего газа, представим себе, что противодавление вдруг резко снижено (хотя бы до нуля). Если скорость истечения к этому времени уже достигла скорости звука, то это никак не отразится на термодинамическом состоянии газа.
Регулируя режим течения газа определенным выбором профиля трубопровода, можно использовать избыточное давление, возникающее в струе при критическом истечении, и реализовать скорости течения, превышающие скорость звука. Физически эта задача заключается в том, чтобы изыскать условия, при которых неупорядоченное молекулярно-тепловое движение в газе, который уже движется со скоростью звука, частично превратить в упорядоченное движение и, таким образом сообщить массе газа скорость, превышающую критическую скорость истечения. С этой целью Лавалем, Стентоном и Франклем были разработаны сверхзвуковые сопла (рис. 9.8).
В сопле Лаваля скорость газа непрерывно растет: в сужающейся части сопла скорость возрастает от нуля до звуковой величины, в расширяющейся части сопла скорость возрастает от звуковой до сверхзвуковой величины. Давление газа по мере приближения к выходу из сопла падает; при уменьшении давления (за критическую величину) скорость истечения растет медленнее, чем уменьшается плотность; поэтому увеличение скорости должно обеспечиваться расширением сопла: выходное сечение больше критического.
|
|
|
| Рис. 9.8 |
При больших относительных перепадах давления понижение температуры газа, текущего по расширяющемуся соплу, бывает очень значительным. Так, например, когда 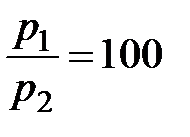 ,
, 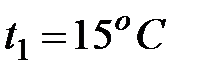 , то температура вытекающей струи воздуха понижается почти на
, то температура вытекающей струи воздуха понижается почти на 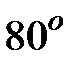 .
.
Течение со сжатием характеризуется уменьшением скорости потока и возрастанием давления, плотности и температуры газа. Согласно уравнению (9.10) убыль кинетической энергии вызывает прирост теплосодержания и повышение температуры:
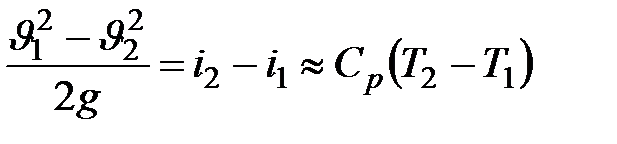
| (9.15) |
Отсюда относительное повышение теплосодержания при адиабатном течении со сжатием до полного затормаживания потока 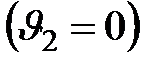 получается равным
получается равным
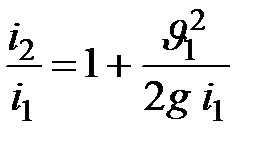
|
Здесь величина 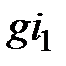 пропорциональна квадрату скорости звука: известно, что скорость звука в газах
пропорциональна квадрату скорости звука: известно, что скорость звука в газах 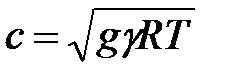 ; с другой стороны,
; с другой стороны, 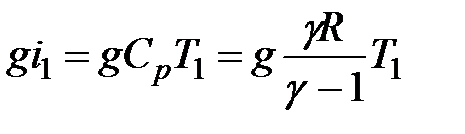 , следовательно,
, следовательно, 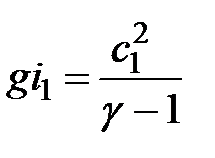 .
.
Итак, относительное повышение теплосодержания зависит только от отношения начальной скорости газа к скорости звука в потоке до торможения газа.
Отношение скорости течения к скорости звука (от которого зависит изменение параметров газа при сжатии) называют числом Маха, или числом Берстоу, и обозначают символом М:
М= 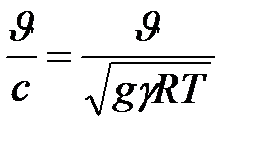
|
Вводя это обозначение в предыдущее уравнение, получаем
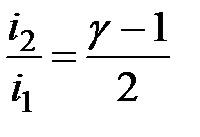 М М 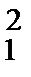
| (9.16) |
Следовательно, если 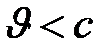 ( М
( М 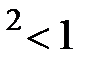 ),то уменьшение сечения сопла приведет к увеличению скорости потока (дозвуковой поток увеличивается с уменьшением сечения сопла). Если же
),то уменьшение сечения сопла приведет к увеличению скорости потока (дозвуковой поток увеличивается с уменьшением сечения сопла). Если же 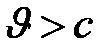 ( М
( М 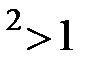 ),тогда расширение сопла приведет к увеличению скорости потока – сверхзвуковой поток будет увеличиваться с увеличением сечения сопла.
),тогда расширение сопла приведет к увеличению скорости потока – сверхзвуковой поток будет увеличиваться с увеличением сечения сопла.
Дата добавления: 2015-08-11; просмотров: 4583;
