Вынужденные электромагнитные колебания. Закон Ома для переменного тока.
Переменный ток можно рассматривать как установившиеся вынужденные электромагнитные колебания в цепи, содержащей резистор, катушку индуктивности и конденсатор. Мыбудем рассматривать квазистационарные токи,для которых мгновенные значения силы тока во всех сечениях цепи практически одинаковы. Для мгновенных значений квазистационарных токов выполняются закон Ома и вытекающие из него правила Кирхгофа.
 Рассмотрим процессы, происходящие в цепи, содержащей последовательно включённые резистор, катушку индуктивности, конденсатор и источник переменной Э.Д.С., изменяющейся по гармоническому закону:
Рассмотрим процессы, происходящие в цепи, содержащей последовательно включённые резистор, катушку индуктивности, конденсатор и источник переменной Э.Д.С., изменяющейся по гармоническому закону:
ε = εo cosw t, (82)
где εo -амплитуда электродвижущей силы.
В цепи возникнет переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения UR, UL, UC . Будем считать, что внутреннее сопротивление источника э.д.с. пренебрежимо мало по сравнению с R. По закону Ома для участка цепи 1- L- R-2 имеем:
IR =( φ1 -φ2)- L(dI/dt) +ε0 cosωt, (83)
где φ2 - φ1 = q/C - мгновенное значение разности потенциалов обкладок
конденсатора, q - его заряд в этот же момент времени, - L(dI/dt) - э.д.с. самоиндукции в контуре. Возьмём производную по времени от обеих частей равенства (145). Учитывая, что dq/dt = I - ток в контуре, получим:
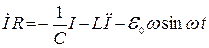
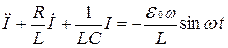 |
(84)
Учитывая, что R/L = 2δ, 1/ (ωC) = ωo2 и введя обозначение - εoω/L = еo уравнение (84) запишем в виде:
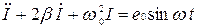 |
(85)
Решение уравнения (85) аналогично решению ранее рассмотренного уравнения (71). Ищем решение уравнения (84) для установившегося режима в виде:
I = Io cos (w t - j ),
где Iо - амплитуда переменного тока в контуре, j - сдвиг фаз между э.д.с. источника тока и силой тока. По аналогии с определением формул (74) и (75) найдём выражения для Iо и j :
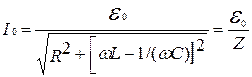 (86)
(86)
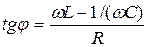 (87)
(87)
Соотношение (86) называется законом Ома для переменного тока. Величина
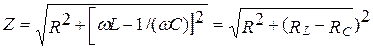 (88)
(88)
называется полным сопротивлением цепи.
RL = ωL - индуктивное сопротивление;
RC = 1/ (ωC) - ёмкостное сопротивление;
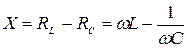 - реактивное сопротивление.Реактивное сопротивление не вызывает тепловых потерь в цепи переменного тока. Оно создаёт сдвиг фаз между током и вынуждающей э.д.с.
- реактивное сопротивление.Реактивное сопротивление не вызывает тепловых потерь в цепи переменного тока. Оно создаёт сдвиг фаз между током и вынуждающей э.д.с.
R - активное сопротивление; за счёт него возникают тепловые потери в контуре.
Падение напряжения на отдельных участках цепи, представленной на рис. 15, можно получить, используя выражение (85):
UC = q/ С = 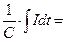 U0C cos(ωt - φ - π/2);
U0C cos(ωt - φ - π/2);
UL = L (dI/dt) = U0L cos(ωt - φ+ π/2);
UR = U0R cos(ωt - φ).
По второму правилу Кирхгофа:
UC + UL + UR = ε0 cosωt
 |
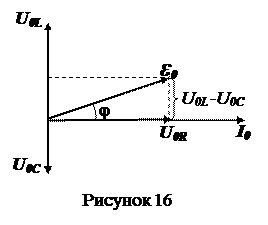 На рисунке 16 представлена векторная диаграмма амплитуд колебаний на всех элементах рассматриваемой цепи (см. рис. 15).
На рисунке 16 представлена векторная диаграмма амплитуд колебаний на всех элементах рассматриваемой цепи (см. рис. 15).
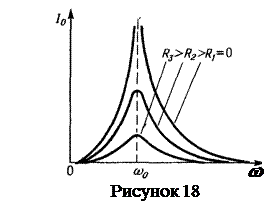
Из выражения (86) следует, что амплитуда тока зависит от частоты вынуждающей э.д.с. (рисунок 18). Максимального значения I0 достигает при частоте ωрез, равной:
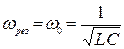 (89)
(89)
( I0 )max = I0рез = ε0 / R (90)
φрез = 0
Явление достижения током максимального значения I0рез при ω = ωрез называется резонансом напряжений. Это вызвано тем, что при ω = ωрез падения напряжений на индуктивном и ёмкостном сопротивлениях достигают максимальных значений равных по модулю и противоположных по фазе, поэтому суммарное падение напряжение на реактивном сопротивлении равно нулю. Падение напряжения на активном сопротивлении максимально, его амплитудное значение
( UL )рез = ( UС )рез (91)
UR0 = ε0 .
Векторная диаграмма для резонанса напряжений приведена на рис.17.
Подставив в формулу (91) значения резонансной частоты и амплитуды напряжений на катушке индуктивности и конденсаторе, получим:
( UL )рез= ( UС )рез= 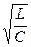 I0 =
I0 = 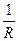
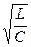 U0 = Q U0,(92)
U0 = Q U0,(92)
где Q - добротность контура.
Так как добротность обычных колебательных контуров больше единицы, то напряжение как на катушке индуктивности, так и на конденсаторе превышает напряжение, приложенное к цепи. Поэтому явление резонанса напряжений используется в технике для усиления колебания напряжения какой-либо определенной частоты. Например, в случае резонанса на конденсаторе, можно получить напряжение с амплитудой QUm ( в данном случае Q - добротность контура, которая может быть значительно больше Um. Это усиление напряжения возможно только для узкого интервала частот вблизи резонансной частоты контура, что позволяет выделить из многих сигналов одно колебание определенной частоты, т. е. на радиоприемнике настроиться на нужную длину волны. Явление резонанса напряжений необходимо учитывать при расчете изоляции электрических линий, содержащих конденсаторы и катушки индуктивности, так как иначе может наблюдаться их пробой.
Дата добавления: 2015-07-18; просмотров: 1524;
