Резонанс

Из выражения (74) следует, что амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При частоте вынуждающей силы, приближающейся к частоте собственных колебаний системы, амплитуда колебаний увеличивается. Частоту изменения вынуждающей силы, при которой амплитуда вынужденных колебаний достигает максимального значения, называют резонансной. Расчёты показывают, что

w_рез = 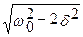(78)

Подставив это значение частоты в выражение ( 74 ), получим формулу амплитуды при резонансе:

А_рез = 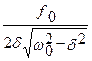(79)

Из выражения (79) следует, что при отсутствии сопротивления среды

резонансная амплитуда обращалась бы в бесконечность. Согласно формуле (78) при r → 0, а следовательно и δ → 0, ω_рез→ω_o.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы показана на рисунке 13 . Отдельные кривые на графике

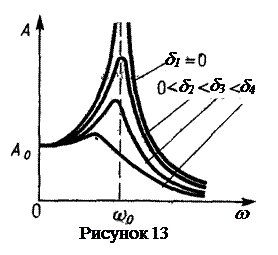соответствуют различным значениям параметра d. В соответствии с выражениями (78) и (79), чем меньше d, тем выше и правее лежит максимум данной кривой. При очень большом затухании (таком, что 2d²>w_о²) выражение для резонансной частоты становится мнимым. Это означает, что при этих условиях резонанс не наблюдается - с увеличением частоты амплитуда вынужденных колебаний монотонно убывает. Изображенная на рисунке 13 совокупность графиков функции (79), соответствующих различным значениям параметра d, называется резонансными кривыми.

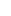
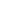
По поводу резонансных кривых можно сделать еще следующие замечания. При стремлении w_о к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному f_о/w_о², т. е. F_o/k. Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F_o. При w → ∞ все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия. Наконец, отметим, что чем меньше d, тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» по­лучается максимум. Из формулы (79) вытекает, что при малом зату­хании (т. е. при d<<w₀) амплитуда при резонансе при­ближенно равна

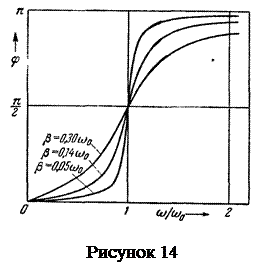А_рез = 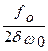(80)

Разделим это выражениена смещение x_о из положе­ния равновесия под действием постоянной силы F₀, учитывая, что x_о =f₀/w_o².

В результате получим:

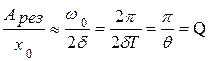(81)

Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резо­нанса превышает смещение системы из положения равновесия под действием постоянной силы той же вели­чины, что и амплитуда вынуждающей силы (это справедливо лишь при небольшом затухании).

Как видно из рис.14, вынужденные колебания от­стают по фазе от вынуждающей силы, причем величина отставания j лежит в пределах от 0 до p. При изменении частоты вынуждающей силы меняется и сдвиг фаз между смещением и вынуждающей силой.

Т.к. tgj = 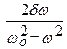, то при w<<w₀ tgj = 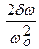, т.е. j ® 0. Следовательно, фаза смещений почти совпадает с фазой вынуждающей силы. С увеличением w, при w®w₀ и tgj ® p/2. Частоте w₀ соответствует j = p/2. Т.е. при резонансе вынужденные колебания отстают по фазе от вынуждающей силы на p/2. Резонансная частота меньше собственной. Следовательно, в момент резонанса j < p/2. При дальнейшем увеличении частоты w, когда w >> w ₀, tgj = -2δ/ω и сдвиг фаз становится равным p. Зависимость j от w при разных значениях d показана графически на рисунке 14.

При слабом затухании w_рез» w₀, и значение j при резонансе можно считать равным p/2.Сдвиг фаз на p/2 при резонансе означает, что вынуждающая сила опережает смещение на Т/4. При этом условии работа вынуждающей силы всегда положительна и приток энергии к колебательной системе максимален.

С явлением резонанса приходится считаться при конструировании машин и различного рода сооружений. Собственная частота колебаний этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий. В противном случае возникают вибра­ции, которые могут вызвать катастрофу. Известны слу­чаи, когда обрушивались мосты при прохождении по ним марширующих колонн солдат. Это происходило потому, что собственная частота колебаний моста оказывалась близкой к частоте, с которой шагала колонна.

Вместе с тем явление резонанса часто оказывается весьма полезным, особенно в акустике, радиотехнике и т.д.