Дифференциальное уравнение волны (волновое уравнение)

Дифференциальное уравнение, решением которого является уравнение волны, называется волновым уравнением. Для его получения необходимо взять частные производные второго порядка по координатам и времени от функции (104). Для гармонической волны, распространяющейся вдоль оси х, получим волновое уравнение в виде:

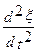= υ² ,

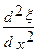где υ = ω/k.

Если волна распространяется вдоль некоторого направления 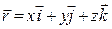, то волновое уравнение примет вид:

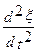= υ²Δξ , (106)

где 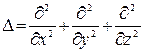- оператор Лапласа.

Волновое уравнение (106) справедливо для любых волн, распространяющихся в однородной изотропной непоглощающей среде.