Интерференция волн. Рассмотрим случай наложения синусоидальных волн, возбуждаемых в однородной и изотропной среде различными источниками
Рассмотрим случай наложения синусоидальных волн, возбуждаемых в однородной и изотропной среде различными источниками. Ограничимся случаем одновременного распространения двух синусоидальных волн, соответствующих одинаково направленным колебаниям частиц среды.
Пусть в точку М пространства приходят две такие волны от точечных
источников S1 и S2:
 ξ1 =
ξ1 = 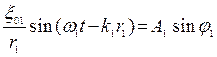
ξ2 = 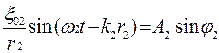
По принципу суперпозиции результирующее колебание в точке М будет:
ξ = ξ1 + ξ2 = А sinφ.
Как было показано ранее (см. сложение одинаково направленных колебаний) амплитуда результирующего колебания определяется из соотношения:
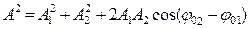 (114)
(114)
Из формулы (196) следует, что амплитуда результирующего колебания зависит от разности фаз Δφ = φ2 - φ1 складываемых волн в точке М:
Δφ = 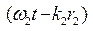 -
- 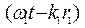 = ( ω2 - ω1 ) t -
= ( ω2 - ω1 ) t - 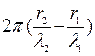 (115)
(115)
Особый интерес представляет наложение когерентных волн. Когерентныминазываются волны, частоты которых равны, а разности фаз постоянны или равны нулю. Явление наложения когерентных волн называется интерференцией.
Если рассматриваемые волны когерентны, то ω1 = ω2 и
φ2 - φ1 =  , (116)
, (116)
где ∆r - разность хода рассматриваемых волн от их источников до точки М.
Из выражения (198) следует, что ∆φ для данной точки пространства величина постоянная. Следовательно, амплитуда колебаний в данной точке пространства также постоянна и в зависимости от ∆φ может принимать значения в пределах:
| А1 - А2 | ≤ А ≤ ( А1 + А2 )
В тех точках пространства, для которых выполняется условие
 ∆φ = 0, 2π, 4π, 6π,…, т.е. 2тπ
∆φ = 0, 2π, 4π, 6π,…, т.е. 2тπ
или (117)
∆r = 0, λ, 2λ, 3λ,…, т.е тλ , ( т = 0, 1, 2, 3, …)
амплитуда колебаний будет максимальна и выражения (199) называются
Дата добавления: 2015-07-18; просмотров: 806;
