Стоячие волны. Особым случаем интерференции являются стоячие волны — это волны, образующиеся при наложении двух бегущих волн

Особым случаем интерференции являются стоячие волны — это волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с оди­наковыми частотами и амплитудами, а в случае поперечных волн и с одинаковой поляризацией. Стоячая волна может быть получена при отражении бегущей волны от препятствия и наложении отражённой волны на бегущую.

Для вывода уравнения стоячей волны предположим, что две плоские волны рас­пространяются навстречу друг другу вдоль оси х в среде без затухания, причем обе волны характеризуются одинаковыми амплитудами и частотами. Кроме того, начало координат выберем в точке, в которой обе волны имеют одинаковую начальную фазу, а отсчет времени начнем с момента, когда начальные фазы обеих волн равны нулю. Тогда соответственно уравнения волны, распространяющейся вдоль положительного направления оси х, и волны, распространяющейся ей навстречу, будут иметь вид:

x (x,t) = Acos(w t – k x)

x (x,t) = Acos(w t+ k x). (119)

Сложив эти уравнения и учитывая, что k= 2p/l, получим уравнение стоячей волны:

ξ = ξ₁ + ξ₂ =2 А coskx coswt = 2А cos(2πx/λ) coswt (120)

Из уравнения стоячей волны (120) вытекает, что все точки стоячей волны колеблются с разными амплитудами А_ст = |2Acos(2px/l)|, зависящими от координаты х рассматриваемой точки. В отличие от бегущей волны, все точки которой совершают колебания с одинаковой амплитудой, но с запаздыванием по фазе (в уравнении бегущей волны фаза колебаний зависит от координаты х рассматриваемой точки), все точки стоячей волны между двумя узлами колеблются с разными амплитудами, но с одинаковыми фазами ( в уравнении стоячей волны аргумент косинуса не зависит от х). При переходе через узел множитель 2Acos(2px/l) меняет свой знак, поэтому фаза колебаний по разные стороны от узла отличается на p,

т. е. точки, лежащие по разные стороны от узла, колеблются в противофазе.

В точках среды, где

2p x/l = ±mp (m = 0, 1, 2, ...), (121)

амплитуда колебаний достигает максимального значения, равного 2А.

В точках среды, где

2px/l= ±(2m+1) 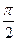(m = 0, 1, 2, ...) (122)

амплитуда колебаний обращается в нуль. Точки, в которых амплитуда колебаний максимальна (А_ст=2А), называются пучностями стоячей волны, а точки, в которых амплитуда колебаний равна нулю (А_ст=0), называются узламистоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Из выражений (121) и (122) получим соответственно координаты пучностей и узлов:

х_пуч = ± m 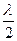, (m = 0, 1, 2, ...) (123)

х_узл = ±(2m+1) 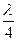. (m = 0, 1, 2, ...) (124)

Из формул (123) и (124) следует, что расстояния между двумя соседними пучностями и двумя соседними узлами одинаковы и равны λ/2. Расстояние между соседними пучностью и узлом стоячей волны равно λ/4.

Рассмотрим пример образования стоячей волны. Если конец веревки закрепить неподвижно, то отраженная в месте крепления веревки волна будет интерферировать с бегущей волной и образует стоячую волну. На границе, где происходит отражение волны, в данном случае возникает узел. Будет ли на границе отражения узел или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения возникает пучность (рис.21, а), если более плотная - узел (рис.21, б). Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную. У границы происходит сложение колебаний с противоположными фазами, в результате чего получается узел. Если же волна отражается от менее плотной среды, то изменения фазы не происходит, и колебания складываются с одинаковыми фазами - образуется пучность. Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, так как падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Поэтому полная энергия результирующей стоячей волны, заключенной между узловыми точками, остается постоянной. Лишь в пределах расстояний, равных половине длины волны, происходят взаимные и превращения кинетической энергии в потенциальную и обратно.