Энергия волны

Пусть плоская незатухающая гармоническая волна распространяется вдоль оси х. Её уравнение имеет вид (104):

x (x,t) = Acos(w t – k x).

Распространение волны сопровождается переносом энергии без переноса вещества. Полная энергия частиц среды, в которой распространяется волна, равна сумме кинетической и потенциальной энергий:

W_к + W_п = W (107)

Рассмотрим объём среды ΔV,возбуждаемый волной. Если плотность среды r , то масса рассматриваемого объёма Δm = ρΔV. Определим кинетическую энергию частиц рассматриваемого объёма:

W_к = 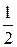т υ² = = 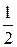ρ ω² A² sin² (ωt - kx) ΔV. (108)

Потенциальная энергия равна работе по упругой деформации среды. Можно показать, что она равна кинетической энергии и также определяется формулой (108). Тогда полная энергия, переносимая волной через объём ΔV,

равна 2 W_к :

W = ρ ω² A² sin² (ωt - kx) ΔV. (109)

Таким образом, в каждом элементе объёма, охваченного волновым движением W_к и W_п являются одинаковыми функциями времени, соответственно и W изменяется с течением времени по такому же закону (сравнить: полная энергия гармонических колебаний не зависит от времени). Эта закономерность справедлива для любых бегущих волн в упругой среде независимо ни от формы их волновых поверхностей, ни от типа деформации среды.

Под объёмной плотностью энергии w упругих волн понимают механическую энергию единицы объёма среды, обусловленную распространением этих волн:

w = W/ DV = ρ ω² A² sin² (ωt - kx) (110)

Потоком энергии Ф_W через какую-либо площадь S называется величина, численно равная энергии, переносимой волной через эту площадь в единицу времени:

Ф_W = W / Δt = wи S, (111)

где и - групповая скорость.

Плотностью потока энергии или вектором Умова называется векторная величина, численно равная энергии, переносимой волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны, , её модуль равен:

j = W/DS×Dt = w и = ρ ω² A² и sin² (ωt - k x)

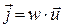(112)

Среднее по времени значение модуля плотности потока энергии называется интенсивностью волны J:

J=|<j>|= |<w>| u = 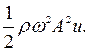(113)

Таким образом, интенсивность волны пропорциональна квадрату её амплитуды.

Единицы энергетических характеристик волны:

[w] = [Дж/м³]; [Ф_W] = [Дж/с)]; [ j ] = [J ] = [Дж/(м^{2 .}с)]