Внутренняя энергия

Внутренняя энергия системы включает в себя:

Кинетическую энергию поступательного, вращательного и колебательного движения частиц;

Потенциальную энергию взаимодействия частиц;

Энергию электронных оболочек атомов;

Внутриядерную энергию.

В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными. Поэтому в дальнейшем под внутренней энергией будем понимать энергию хаотического движения молекул и атомов, включающую энергию поступательного, вращательного и колебательного движений как молекулярного, так и внутримолекулярного, а также потенциальную энергию сил взаимодействия между молекулами.

Кинетическая энергия молекул является функцией температуры, значение потенциальной энергии зависит от среднего расстояния между молекулами и, следовательно, от занимаемого газом объема V, т.е является функцией V. Поэтому внутренняя энергия U есть функция состояния тела.

Величина 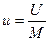, называется удельной внутренней энергией (Дж/кг) и представляет собой внутреннюю энергию единицы массы вещества.

Поскольку внутренняя энергия есть функция состояния тела, то она может быть представлена в виде функции двух любых независимых параметров, определяющих это состояние:

.

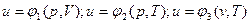Ее изменение в термодинамическом процессе 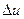не зависит от характера процесса и определяется только начальным и конечным состояниями тела:

,

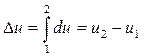где 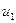- значение внутренней энергии в начальном состоянии;

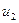- в конечном.

Для задач технической термодинамики важно не абсолютное значение внутренней энергии, а ее изменение в различных термодинамических процессах. Поэтому начало отсчета внутренней энергии может быть выбрано произвольно. Например, в соответствии с международным соглашением для воды за нуль принимается значение внутренней энергии при температуре 0,01 ⁰С и давление 610,8 Па, а для идеальных газов – при 0 ⁰С вне зависимости от давления.

Работа

Работа (в механике) – произведение действующей на рабочее тело силы на путь ее действия.

Передачу энергии от одного тела к другому, связанную с изменением объема рабочего тела, с перемещением его во внешнем пространстве или с изменением его положения, называют работой.

В производстве работы всегда участвуют два тела или больше. Первое тело, производящее работу, отдает энергию, второе тепло получает энергию.

Определение работы расширения:

Рассмотрим газ массой М и объемом V, заключенный в эластичную оболочку с поверхностью F.

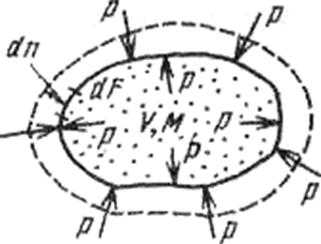
Рис. 1.2. К определению работы расширения

Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая при этом работу против внешнего давления р, оказываемого на него средой. Газ действует на каждый элемент оболочки dF, с силой, равной pdF и, перемещая ее по нормали к поверхности на расстояние dn, совершает элементарную работу pdFdn. Общую работу, совершенную в течение бесконечно малого процесса, получим, интегрируя, данное выражение по всей поверхности F оболочки: 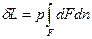(Различие символов δ и d у бесконечно малых величин 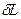и dU связано с тем, что величина 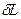в отличии от dU не является полным дифференциалом.)

Из рисунка видно, что изменение объема dV выражается в виде интеграла по поверхности: 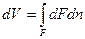, следовательно .

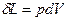При конечном изменении объема работа против сил внешнего давления, называемая работой расширения, равна

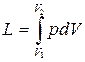. (1.7)

Отсюда следует, что 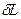и dV всегда имеют одинаковые знаки:

Если dV>0, то и 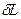>0, т.е. при расширении работа тела положительна, при этом тело само совершает работу;

Если же dV<0, то и 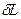<0, т.е. при сжатии работа тела отрицательна. Это означает, что не тело совершает работу, а на его сжатие затрачивается работа извне.

Единицей измерения работы в СИ является джоуль (Дж).

Отнеся работу расширения к 1 кг массы рабочего тела, получим

; .

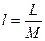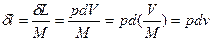Величина l, представляющая собой удельную работу, совершаемую системой, содержащей 1 кг газа, равна

.

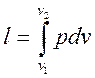Вышеперечисленные формулы справедливы только для равновесных процессов, при которых давление рабочего тела равно давлению окружающей среды.

В термодинамике для исследования равновесных процессов широко используют p,v-диаграмму. Поскольку состояние термодинамической системы определяется двумя параметрами, то на p,v диаграмме оно изображается точкой. На рис. 1.3 точка 1 соответствует начальному состоянию системы, точка 2 – конечному, а линия 1-2 процессу расширения рабочего тела от v₁ до v₂.

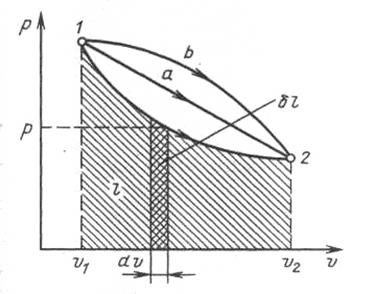
Рис. 1.3. Графическое изображение работы в

p,v- координатах

При бесконечно малом изменении объема dv площадь заштрихованной вертикальной полоски равна 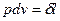. Следовательно, работа процесса 1-2 изображается площадью, ограниченной кривой процесса, осью абсцисс и крайними ординатами. Таким образом, работа изменения объема эквивалентна площади под кривой процесса в диаграмме p,v.

Каждому пути перехода системы из состояния 1 в состояние 2 (например, 1-2, 1-а-2 или 1-b-2) соответствует своя работа расширения: l_1b2>l_1a2>l₁₂. Следовательно, работа зависит от характера термодинамического процесса, а не является функцией только исходного и конечного состояния системы. С другой стороны, 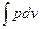зависит от пути интегрирования и, следовательно, элементарная работа δl не является полным дифференциалом.

Поскольку величина δl пропорциональна увеличению объема, то в качестве рабочих тел, предназначенных для преобразования тепловой энергии в механическую, целесообразно выбирать такие, которые обладают способностью значительно увеличивать свой объем (водяной пар в энергетике, газообразные продукты сгорания в ДВС).