Уравнение бегущей волны.

Бегущими волнами называются волны, которые переносят в пространстве энергию.Независимо от физической природы все волны подчиняются одинаковым закономерностям и описываются одинаковыми математическими уравнениями.

Для описания колебания точек среды в любой момент времени при распространении волны вводится волновая функция x (r,t), являющаяся функцией координат и времени. Выражение, определяющее эту функцию, и есть уравнение волны. Для вывода уравнения бегущей волны рассмотрим простейший случай: плоская волна, распространяется вдоль оси х. Источник колебаний находится в точке х = 0 (рис.19)и колеблется по гармоническому закону:

x (0,t) = A(0) cos w t. (101)

Частица В среды колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на время t, необходимое для прохождения волной расстояния х : t = х/v, где v - скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид

x (x,t) = A cos w ( t - x/v ). (102)

Уравнение (102) и есть уравнение бегущей плоской гармонической волны. Если в среде не происходит потери энергии волны за счёт её поглощения, то амплитуда плоской волны А остаётся постоянной: А(0) = А(х). В уравнении (102) начальная фаза колебаний источника волн принята за 0. Если плоская гармоническая волна распространяется против оси х, то её уравнение имеет вид:

x (x,t) = Acosw ( t + x/v )(103)

Уравнение (102) можно преобразовать, используя выражение (98):

x (x,t) = Acos(w t – k x) = Acos(w t –2π x/λ)(104)

Уравнение сферической волны — волны, волновые поверхности которой имеют вид концентрических сфер, имеет вид:

x (x,t) = 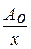cos(wt –kx), (105)

Из уравнения сферической волны следует, что её амплитуда даже при отсутствии поглощения средой убывает с расстоянием по закону 1/х. Уравнение (105) справедливо лишь для х, значительно превышающих размеры источника (тогда источник колебаний можно считать точечным).

Рассмотренные уравнения описывают как продольные, так и поперечные волны.