Некоторые свойства электромагнитной волны
Электромагнитные волны представляют собой распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы 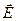 и
и 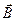 перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис. 46).
перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис. 46).
Так как векторы 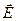 ,
, 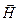 и
и 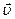 образуют правовинтовую
образуют правовинтовую  тройку векторов, то их взаимная ориентация подчиняется правилу:
тройку векторов, то их взаимная ориентация подчиняется правилу:
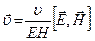
Для электромагнитной волны справедливы все формулы, закономерности и соотношения, которые были отмечены ранее для волновых процессов. Поэтому, согласно выражению (105), уравнение синусоидальной плоской электромагнитной волны, распространяющейся вдоль направления 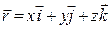 , можно записать в виде:
, можно записать в виде:
 Е (r,t) =Е0 cos(w t – kr)
Е (r,t) =Е0 cos(w t – kr)
(125)
Н (r,t) =Н0 cos(w t – kr)
Волновое уравнение такой электромагнитной волны имеет вид:

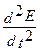 = υ2
= υ2 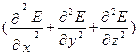 ,
,
(126)
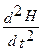 = υ2
= υ2 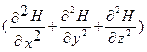 ,
,
где υ - фазовая скорость электромагнитной волны. С помощью уравнений Максвелла было показано, что электромагнитные волны распространяются в веществе с конечной скоростью, определяемой по формуле:
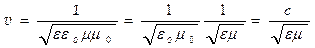 . (127)
. (127)
Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные:
ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м.
Скорость электромагнитных волн в вакууме (ε = μ = 1):
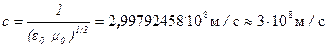 .
.
Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных. Равенство скорости распространения электромагнитных волн в вакууме скорости света в вакууме позволило Максвеллу предположить, что свет имеет электромагнитную природу.
Электромагнитная волна называется монохроматической,если проекции её векторов 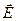 и
и 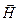 на оси прямоугольной системы координат совершают гармонические колебания одинаковой частоты.
на оси прямоугольной системы координат совершают гармонические колебания одинаковой частоты.
В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Объемная плотность энергии электромагнитного поля в линейной изотропной среде
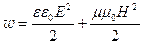 , (128)
, (128)
В электромагнитной волне модули напряженности магнитного поля 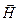 и напряженности электрического поля
и напряженности электрического поля 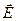 в каждой точке пространства связаны соотношением
в каждой точке пространства связаны соотношением
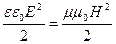 . (129)
. (129)
Из уравнения (129) следует, что
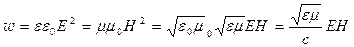 , (130)
, (130)
где с –скорость электромагнитных волн в вакууме.
Электромагнитные волны переносят энергию.
Плотностью потока энергии называют энергию, переносимую волной за единицу времени через единицу площади. Вектор плотности потока электромагнитной энергии называется вектором Умова-Пойнтинга 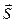 . Согласно формуле (112), имеем:
. Согласно формуле (112), имеем:
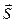 =
= 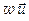 =
= 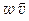 .
.
Для монохроматической волны групповая и и фазовая υ скорости равны. Подставляя сюда выражения (128) для w и (127) для υ, можно получить:
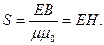
Так как векторы 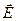 и
и 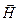 взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора
взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора 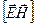 совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН:
совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН:
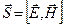 (131)
(131)
Единицей плотности потока энергии в СИ является Ватт на квадратный метр (Вт/м2).
Так как интенсивность бегущей электромагнитной волны это физическая величина J, равная модулю среднего значения вектора Умова- Пойнтинга за период его полного колебания, то
:
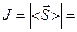 |
| 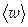 υ|, (132)
υ|, (132)
где 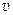 -фазовая скорость,
-фазовая скорость, 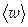 -среднее значение объемной плотности энергии. Согласно выражению (113), интенсивность волны пропорциональна квадрату амплитуды. Так как
-среднее значение объемной плотности энергии. Согласно выражению (113), интенсивность волны пропорциональна квадрату амплитуды. Так как 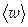 , согласно выражению (130), пропорциональна Е02 , то этот вывод справедлив и для электромагнитной волны: интенсивность электромагнитной волны пропорциональна квадрату амплитуды.
, согласно выражению (130), пропорциональна Е02 , то этот вывод справедлив и для электромагнитной волны: интенсивность электромагнитной волны пропорциональна квадрату амплитуды.
Дата добавления: 2015-07-18; просмотров: 1000;
