Интерференция волн

Если в веществе распространяются волны малой амплитуды, то, проходя одновременно через некоторую область пространства, они подчиняются принципу суперпозиции. При наложении друг на друга волны не искажаются: разойдясь, они не несут на себе следов прошедшего взаимодействия. Суперпозиция волн приводит к характерным для волнового движения явлениям: интерференции и дифракции.

· Интерференция– явление наложения в волновой зоне конечного числа (двух или более) волн, в результате чего в различных точках пространства происходит усиление или ослабление амплитуды результирующей волны.

· Дифракция– любое отклонение волн от прямолинейного распространения, в узком смысле – это огибание волнами препятствий.

· Когерентнымиволнаминазывают волны, имеющие одинаковую частоту и неизменную во времени разность фаз для всех точек пространства.

Рассмотрим процесс наложения двух плоских когерентных волн с частотой w, распространяющихся от источников I₁ и I₂. Предположим, что амплитуды волн А равны между собой, начальные фазы колебаний источников равны нулю. Волны (см. рис. 1.17) проходят до точки наблюдения М различные пути S₁ и S₂, и возбуждают в ней колебания, которые описываются уравнениями:

.

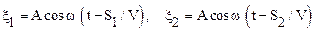В формулах (1.65) величина t соответствует времени, прошедшему от начала работы источников волн, V – скорость распространения волн.

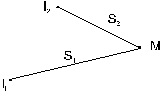
Рис. 1.17. К расчету интерференционного поля

При условии, что оба колебания происходят в одном направлении, амплитуда результирующего колебания в точке М может быть определена на основании принципа суперпозиции (см. (1.40)):

.

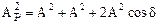Из соотношения (1.66) видно, что амплитуда А_Р колебаний в точке наблюдения при прочих, указанных выше условиях зависит от величины слагаемого 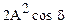, а конкретней, от множителя cosd.

Величину 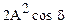называют интерференционным членом, d=Ф₂-Ф₁ – разностьюфаз Ф₁ и Ф₂ колебаний, вызванных первой и второй волной в точке наблюдения:

.

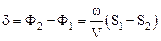Интенсивность волны I пропорциональна квадрату ее амплитуды A, т. е. I~A², поэтому для интенсивности результирующего колебания (см.(1.66)) можно записать:

.

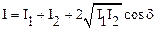Величину D=S₁-S₂ называют разностьюхода волн. Очевидно, что при условиях, указанных выше, разность хода D и разность фаз d определяются положением точки М, а значит, в различных точках пространства результирующее колебание будет иметь различную амплитуду и интенсивность. Таким образом, при наложении когерентных волн в волновом поле образуется некоторое распределение интенсивности колебаний, а значит, – неравномерное распределение энергии колебаний. Распределение амплитуды результирующего колебания, характеризуемое положением минимумов и максимумов колебаний, дает интерференционную картину. Интерференционная картина неподвижна, несмотря на то, что она образована бегущими волнами. Это связано с тем, что для когерентных волн разность фаз колебаний d в точке М, а, значит, и амплитуда колебаний остается постоянной с течением времени.

В зависимости от знака интерференционного члена 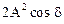(знака функции косинуса) интенсивность колебаний в точке наблюдения М может быть больше суммы интенсивностей I₁ и I₂ колебаний от источников (если cosd>0), или меньше этой суммы (cosd<0). Особенно отчетливо интерференция наблюдается при равенстве интенсивностей налагающихся волн: I₁=I₂, в этом случае наибольшее значение I равно 2I₁, наименьшее – нулю.

Вернемся к формуле (1.67), которую запишем, используя разность хода, как

.

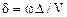Проведем следующие преобразования

.

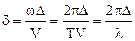Из последнего следует, что если разность хода D для некоторой точки наблюдения М равна целому числу длин волн D=nl, то разностьфаз d будет кратна 2p (d=2pn); в этом случае говорят, что разностьфаз составляет четое число p. Колебания, возбуждаемые первой и второй волной в этой точке, будут происходить синхронно и амплитуда колебаний в ней будет наибольшей: в точке М располагается интерференционный максимум.

Условие (1.70) окончательно можно сформулировать так:

· интерференционныймаксимум в некоторой точке пространства наблюдается при условии, что разность хода волн до нее составляет целое число длин волн (или четное число длин полуволн):

.

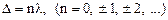Несложно видеть, что если разность хода волн составляет нечетное число длин полуволн, то в точке наблюдения имеется интерференционныйминимум:

,

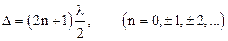здесь l – длина волны в среде, в которой распространяются волны. Из соотношений (1.70) и (1.71) следует, что в этом случае разность фаз равна нечетному числу p, т. е.

.

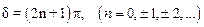Если разность фаз d колебаний в точке М меняется случайным образом, то в результате усреднения по времени (время усреднения много больше периода колебаний) интерференционный член обращается в ноль, поскольку среднеезначение косинуса равно нулю. В этом случае соотношение (1.66) дает

,

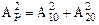или

,

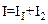т. е. интерференционная картина отсутствует, и в точках пространства наблюдается равномерное распределение энергии колебаний.