Распространение, отражение и преломление волн

Формально процесс распространения волн объясняется принципом Гюйгенса.

· ПринципГюйгенса утверждает: каждая точка среды, до которой доходит волна, становится источником вторичных волн. Поверхность, огибающая в некоторый момент вторичные фронты, указывает положение фронта распространяющейся волны в этот момент времени. Огибающей называют поверхность, касательную ко всем вторичным фронтам.

Принцип Гюйгенса позволяет достаточно просто объяснить явления преломления и отражения волн. В соответствии с принципом, наложение вторичных волн, образованных на границе раздела сред приводит к появлению в первой среде отраженной волны, а во второй – преломленной. Напомним, что в волновой механике направление распространения волны в пространстве задает волновой луч. При наличии отражающих и преломляющих поверхностей используют так называемые углы падения и преломления.

· Уголпадения – это угол между волновым лучем падающей волны и нормалью к границе раздела сред в точке падения.

· Уголпреломления – это угол между нормалью к границе раздела сред в точке падения волнового луча и волновым лучом преломленной волны.

Рассмотрим явление преломления волн. Пусть элемент плоского волнового фронта AС (см. рис. 1.13), распространяясь в однородной среде со скоростью V₁, падает сверху на плоскую границу раздела сред ОО. Предположим, что скорость волны во второй среде V₂ меньше, чем ее скорость V₁ в первой среде. Построим положение огибающей вторичных волн во второй среде для промежутка времени, соответствующего приходу точки С фронта на границу раздела сред. Очевидно, что это время t равно BC/V₁. За время t вторичная волна пройдет во второй среде расстояние AD, равное

V₂t=BC×V₂/V₁.

Рис. 1.13. Преломление волны на границе раздела сред. АС – фронт падающей волны, ВD- фронт преломленной волны

Из чертежа (рис. 1.13) видно, что:

.

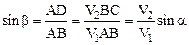Полученный результат позволяет сформулировать закон преломления волн, который утверждает, чтоотношение синуса угла падения к синусу угла преломления равно отношению скорости волны во второй среде к ее скорости в первой среде:

.

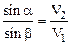Примем без доказательства следующее утверждение: луч падающий, луч преломленный и нормаль, восстановленная в точке падения волны на границу преломляющей среды, лежат в одной плоскости.

Законпреломления волн содержит два утверждения:

· луч падающий, луч преломленный и нормаль, восстановленная в точке падения волны на границу преломляющей среды, лежат в одной плоскости.

· Отношение синуса угла падения к синусу угла преломления равно отношению скорости волны во второй среде к ее скорости в первой среде.

Соотношение (1.64) есть математическое выражение закона преломления.

Рассмотрим теперь явление отражения волн. Пусть часть плоского волнового фронта AF (см. рис. 1.14), распространяясь в однородной среде со скоростью V, падает на плоскую отражающую поверхность ОО.

Построим огибающую вторичных отраженных волн в момент времени, когда точка F фронта достигнет отражающей поверхности в точке В. К этому моменту времени весь участок фронта AF полностью отразится от поверхности ОО. Вторичные сферические волны будут иметь различные радиусы, поскольку они начинают распространяться в различные моменты

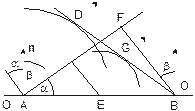
Рис. 1.14. Отражение волны от плоской поверхности

времени, соответственно достижению точками фронта поверхности ОО. Радиусы полусфер равны расстояниям, которые проходят фронты вторичных волн от их источников, расположенных на границе раздела сред. Для волны, испущенной в точке А, радиус фронта равен AD, для точки Е он равен EG, для точки В – нулю. Из равенства треугольников AFB и ADB следует, что угол падения a равен углу отражения b.

· Законотраженияволн, как и закон преломления, содержит два утверждения:

1. Луч падающий, луч отраженный и нормаль, восстановленная в точке падения волны на границу преломляющей среды, лежат в одной плоскости.

2. Угол падения волны на отражающую поверхность равен углу отражения.

Математическое выражение закона отражения таково:

a=b.