Уравнениеплоской волны

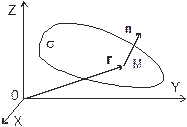
Рис. 1.12. К выводу уравнения бегущей плоской волны

Рассмотрим общий случай, когда распространение колебаний, заданное направляющим вектором n, не совпадает с какой-либо из пространственных осей координат. Пусть в момент времени t=0 в начале координат – точке О, возникают гармонические колебания величины x, описываемые уравнением

.

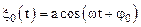Благодаря конечной скорости V распространения волны в пространстве, колебания в точке М будут запаздывать во времени по отношению к колебаниям в точке О на время t=ℓ/V, равное времени распространения волны от источника до точки М. С учетом запаздывания волна, распространяющаяся вдоль направления n, описывается уравнением

,

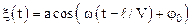где ℓ – расстояние от начала координат до точки наблюдения. Это расстояние, как видно из рисунка 1.12, равно проекции радиус-вектора r точки наблюдения на направление n:

.

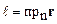Уравнение (1.53) можно записать так:

.

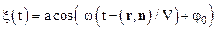Полученное уравнение является уравнениемгармонической волны, распространяющейся (бегущей) в направлении, заданном вектором n. Очевидно, что функция, описывающая бегущую волну, содержащая периодическую функцию косинуса или синуса, является периодической функцией двух аргументов: времени t и координаты Х.

· Гармоническаяволна– это волна, соответствующая распространению гармонических колебаний.

· Амплитудаволны– наибольшее значение колеблющейся величины.

· Фазаволны– величина 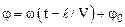или j= 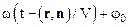, равная аргументу функции косинуса (или синуса) в уравнении волны.

Отметим, что фаза колебания, приходящего от источника в некоторую точку пространства, увеличивается монотонно и линейно с течением времени, а при увеличении расстояния от источника до точки наблюдения фаза уменьшается.

· Начальная фазаволныj₀ – фаза в момент времени t=0; очевидно j₀=j(t=0).

Используя общепринятое обозначение для так называемого волнового вектора k (k=wn/V), преобразуем уравнение волны (1.53) к виду:

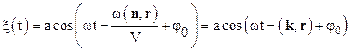
Очевидно, что уравнениеволны распространяющейся вдоль оси Х, имеет вид:

,

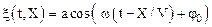или

,

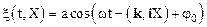здесь k и iX – волновой вектор и радиус-вектор точки наблюдения с координатой Х.

Несложно показать, что уравнениеволны распространяющейся в направлении, противоположном направлению оси Х, имеет вид:

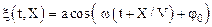. (1.56а)

· Волновойвектор – вектор, определяемый соотношением .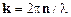

· Волновоечисло – это модуль волнового вектора: 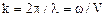. Волновое число показывает, сколько длин волн укладывается на отрезке длиной 2p метров.

Используя понятие волнового числа, уравнению волны бегущей вдоль оси х можно придать симметричный вид:

.

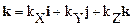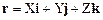Наконец, учитывая разложение векторов k и r по осям координат: и , запишем уравнение (1.54) следующим образом:

.

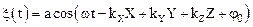Из аналитической геометрии известно, что всякое уравнение первой степени с тремя переменными X,Y,Z вида

(*)

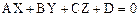определяет в пространстве плоскость. Сравнение выражения (1.58) с (*) показывает, что коэффициент D играет роль фазы волны и содержит в себе зависимость от времени. Таким образом, уравнение (*) определяет положение некоторой плоскости в каждый момент времени. Во всех точках этой плоскости, называемой волновой поверхностью, фазы волны одна и та же.